相關知識
離散對數的概念:
原根:如果 a是素數 p的一個原根,那么數值:
amod p, a^ 2mod p,…, a^( p-1)mod p
是各不相同的整數,且以某種排列方式組成了從 1到 p-1的所有整數。
離散對數:如果對於一個整數 b和素數 p的一個原根 a,可以找到一個唯一的指數 i,使得:
b=( a的i次方)mod p其中 0≦ i≦ p-1
那么指數 i稱為 b的以 a為基數的模p的離散對數。
Diffie-Hellman算法的有效性依賴於計算離散對數的難度,其含義是:當已知大素數 p和它的一個原根 a後,對給定的 b,要計算 i,被認為是很困難的,而給定 i計算 b卻相對容易 。
算法原理
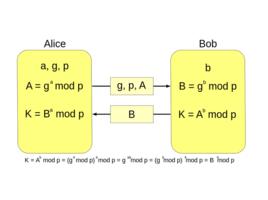
設 A, B 兩方進行通信前需要交換密鑰,首先 A, B 共同選取 p 和 a 兩個素數,其中 p 和 a 均公開。之後 A 選擇一個自然數 Xa,計算出 Ya,Xa 保密,Ya 公開;同理,B 選擇 Xb 並計算出 Yb,其中 Xb 保密,Yb 公開。之後 A 用 Yb 和 Xa 計算出密鑰 K,而 B 用 Ya 和 Xb 計算密鑰 K,流程如下:
 Diffie-Hellman密鑰交換算法
Diffie-Hellman密鑰交換算法+-------------------------------------------------------------------+
Global Pulic Elements
p prime number
a prime number, a < p
+-------------------------------------------------------------------+
User A Key Generation
Select private Xa Xa < p
Calculate public Ya Ya = a^Xa mod p
+-------------------------------------------------------------------+
User B Key Generation
Select private Xb Xb < p
Calculate public Yb Yb = a^Xb mod p
+-------------------------------------------------------------------+
Calculation of Secret Key by User A
Secret Key K K = Yb^Xa mod p
+-------------------------------------------------------------------+
Calculation of Secret Key by User B
Secret Key K K = Ya^Xb mod p
+-------------------------------------------------------------------+
下面證明,A 和 B 計算出來的密鑰 K 相同。
K = Yb^Xa mod p = (a^Xb mod p)^Xa mod p = a^(Xa * Xb) mod p
根據上述求模公式 = (a^Xa mod p)^Xb mod p = Ya^Xb mod p
上面一共出現了 a, p, Xa, Ya, Xb, Yb, K 共 7 個數,其中:
•公開的數:a, p, Ya, Yb
•非公開數:Xa, Xb, K
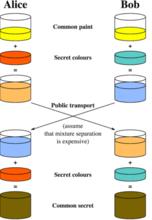
通常情況下,a 一般為 2 或 5,而 p 的取值非常大,至少幾百位,Xa 和 Xb 的取值也非常大,其複雜度至少為O(p^0.5)。對於攻擊者來說,已知 Ya,Xa 的求解非常困難,同理 Xb 的求解也很困難,所以攻擊者難以求出 K,所以 DH 能夠保證通信雙方在透明的信道中安全的交換密鑰。下圖非常形象的描述密鑰交換流程:
套用
DH在TLS中的套用
DH算法作為一種密鑰協商機制,可以用於TLS協定當中。
如果在DH互動過程中Alice和Bob始終使用相同的私鑰,就會導致後續產生的共享密鑰是一樣的,如果有嗅探者截獲通信雙方的所有數據,由於都是同一個密鑰加密所得,一旦被破解,後續的通信將全部暴露。
為了保證安全性,必須引入前向保密,即Forward Secrecy。其基本實現思路就是在Alice和Bob在選擇各自的私鑰是引入隨機性,也印證了那句話:要用發展的眼光看問題,不能一成不變 。
事實上FS在諸多加密協定中套用廣泛,比如IKEv2和802.11i密鑰分發中的4-way握手,無一不引入此方法。
那么問題來了,TLS中哪一個才是最安全的cipher呢?就目前而言,最安全的三個候選者如下:
•TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384_P521
•TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384_P384
•TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384_P256