基本概念
在貝葉斯網路的學習過程中,經常會遇到D分離(D-Separation)這個概念,D分離是尋找網路節點之間的條件獨立性的一種方法或者說一種問題的簡化處理的技巧。採用D分離技術,在用貝葉斯網路進行預測,診斷推理等方面,可以提高計算速度,減少計算複雜性。
原理
對於給定的結點集ε,如果對貝葉斯網中的結點Vi和Vj之間的每個無向路徑,在路徑上有某個結點Vb,如果有屬性:
(1)Vb在ε中,且路徑上的兩條弧都以Vb為頭(即弧在Vb處開始(出發));
(2)Vb在ε中,路徑上的一條弧以Vb為頭,一條以Vb為尾 ;
(3)Vb和它的任何後繼都不在ε中,路徑上的兩條弧都以Vb為頭(即弧在Vb處結束);
則稱Vi和Vj 被Vb結點阻塞。
如果Vi和Vj被證據集合ε中的任意結點阻塞,則稱Vi和Vj是被ε集合D分離,結點Vi和Vj條件獨立於給定的證據集合ε,即P(Vi|Vj,ε) =P(Vi|ε)和P(Vj|Vi,ε) =P(Vj|ε),表示為:I(Vi,Vj|ε) 或I(Vj,Vi|ε) 。
無向路徑:DAG圖是有向圖,所以其中的路徑也應該是有向路徑,這裡所指的無向路徑是不考慮DAG圖中的方向性時的路徑。
條件獨立:如具有以上三個屬性之一,就說結點Vi和Vj條件獨立於給定的結點集ε。
阻塞:給定證據集合ε,當上述條件中的任何一個滿足時,就說Vb阻塞相應的那條路徑。
D分離:如果Vi和Vj之間所有的路徑被阻塞,就叫證據集合ε可以D分離Vi和Vj。D分離的實質就是尋找貝葉斯網中的條件獨立語義,以簡化推理計算。
三種情況獨立分析
情況一
tail-to-tail
節點c連線的是兩個箭頭的尾部,如圖:
 D分離
D分離可知,P(a,b,c)=P(a|c)*P(b|c)*P(c)(1)
現在我們求P(a,b),如果P(a,b)=P(a)*P(b),則a和b是在c條件下獨立分布的。分兩種情況進行討論:
(1)c值不作為觀察點。令(1)式對c求積分,消去c值,考慮c是離散的情況,可得
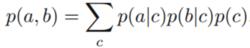 D分離
D分離可以看到,與P(a,b)=P(a)*P(b)不等,所以a和b不是c條件獨立的。
(2)c值作為觀察點(即以c作為條件)。則可以知道c取某個c狀態的機率為P(c),c條件下a和b發生的機率為P(a,b|c)。由下式:
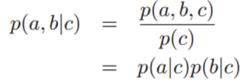 D分離
D分離可得a和b是c條件下獨立的。
情況二
head-to-tail
 D分離
D分離可知,p(a,b,c)=p(a)*p(c|a)*p(b|c) (2)
同樣分兩種情況進行討論:
(1)c值不作為觀察點。對(2)式(考慮c是離散的情況)積分可得:
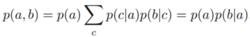 D分離
D分離可知,a和b不是c條件獨立的。
(2)c值作為觀察點。則圖模型表示為:
 D分離
D分離c條件下a和b發生的機率為P(a,b|c)。由下式:
 D分離
D分離可知,a和b是c條件下獨立的。
情況三
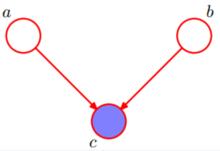
head-to-head
 D分離
D分離可知 p(a,b,c)=p(a)*p(b)*p(c|a,b) (3)
同理,分兩種情況討論:
(1)c值不作為觀察點。由於所有p(c|a,b)相加和=1,所以有(3)式消去c,可得p(a,b)=p(a)*p(b),即a與b是條件獨立的。
(2)c值作為觀察點。
 D分離
D分離所以有:
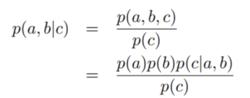 D分離
D分離最後不能因式分解成p(a)*p(b)的形式,所以a與b不是c條件獨立的。
基於D-Seperation的獨立分析
D-Separation是一種用來判斷變數是否條件獨立的圖形化方法。相比於非圖形化方法,D-Separation更加直觀,且計算簡單。對於一個DAG(有向無環圖)E,D-Separation方法可以快速的判斷出兩個節點之間是否是條件獨立的。
對於較為複雜的DAG圖,我們可以給出一個普遍意義上的結論,也就是D-Seperation。對於DAG圖E,如果A,B,C是三個集合(可以是單獨的節點或者是節點的集合),為了判斷A和B是否是C條件獨立的,我們考慮E中所有A和B之間的無向路徑。對於其中的一條路徑,如果她滿足以下兩個條件中的任意一條,則稱這條路徑是阻塞(block)的:
(1)路徑中存在某個節點X是head-to-tial或者tail-to-tail節點(情況一和情況二),並且X是包含在C中的;
(2)路徑中存在某個節點X是head-to-head節點(情況三),並且X或X的兒子是不包含在C中的;
如果A,B間所有的路徑都是阻塞的,那么A,B就是關於C條件獨立的;否則,A,B不是關於C條件獨立的。
實例
根據D-Seperation分隔定理,我們可以很容易的判斷是否是條件獨立的。
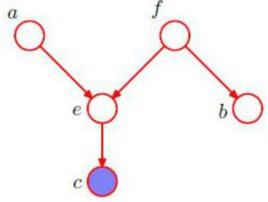
判斷圖中a,b是否是c條件獨立的:
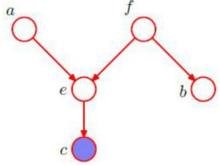 D分離
D分離上圖中a到b只有一條路徑a->e->f->b。考慮路徑上的點e和f,e是head-to-head類型的,且e的兒子節點就是c,根據(b),e是阻斷的。所以a和b是c條件下獨立的。
現在如果要判斷a和b是否是f下條件獨立的。同樣的方法,考慮路徑a->e->f->b上的所有節點。節點e是head-to-head類型的,e和她的兒子節點c都不在f中,所以e不是阻斷路徑的節點。節點f是tail-to-tail節點,且f就在f節點中,所以f節點阻斷了路徑。結論:a和b是f下條件獨立的。
D-Seperation還可以用來證明獨立同分布和馬爾科夫邊界等 。