粒度分離簡介
粒度分離在選礦廠很常見，通常包括篩分作業和分級作業兩大類。
篩分
所謂篩分，就是使鬆散物料通過單層或多層篩面分成多個不同粒度級別的過程，它是利用篩分機械（篩子）的篩面進行粒度分離。按照篩面的運動特性及篩面的形狀可將篩子分為很多種，常見的有：
（1）固定篩。如固定棒條篩、固定細篩、弧形篩等。
（2）運動篩。如搖動篩、直線振動篩、旋轉篩等。
篩分是利用篩面比較嚴格地按顆粒的幾何尺寸進行粒度分離，因此分離的精度高。
篩分作業的目的就是分出入篩物料中粒度比篩孔尺寸小的那部分細粒級別。理想的情況是，粒度比篩孔尺寸小的所有顆粒都進入篩下物中，粒度比篩孔尺寸大的所有顆粒都留在篩面上形成篩上物。然而在實際生產中，由於多種因素的影響，篩上物中總是或多或少地殘留～些粒度比篩孔尺寸小的細顆粒，而篩下物中有時也會因篩面磨損或操作不當混入一些粒度比篩孔尺寸大的粗顆粒。為了描述篩分作業完成的不完善程度，在實際工作中引入了篩分效率的概念。
所謂篩分效率，就是通過篩分實際得到的細粒級別的質量占入篩物料中所含的粒度小於篩孔尺寸的那部分物料的質量百分數。如果用Q、Q、Q和α、β、θ分別代表人篩物料、篩下物、篩上物的質量和入篩物料、篩下物、篩上物中粒度小於篩孔尺寸的那部分物料的質量分數，則根據定義，篩分效率E的計算式為：
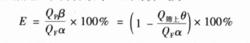篩分效率E的計算式（1）在實際生產中，由於直接測定Q和Q比較困難，所以常常根據篩分過程中物料量的平衡關係進行間接測定和計算篩分效率。
在物料的篩分過程中，存在如下的物料量平衡關係：
Q=Q+Q
Qα=Qθ+Qβ
由上述兩式可推導出
Q/Q=（α-θ）/（β-θ）
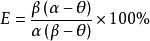粒度分離將上式代圖式（1）得 上述計算出來的篩分效率稱為總篩分效率，即用小於篩孔的所有物料計算出來的篩分效率。
在研究篩分過程時發現，物料中篩下級別的粒級組成對篩分效率影響很大，細粒（易篩顆粒）容易透過篩孔，難篩顆粒很難透過篩孔，因而容易殘存在篩面上。如果按各個粒級來計算篩分效率，則細粒部分的篩分效率要高些，而難篩顆粒的篩分效率要低些。因此，把按照篩下產品中某一級別物料的質量與入篩物料中同一級別物料的質量之比的百分數稱為部分篩分效率。部分篩分效率計算公式同總篩分效率式，只不過此時α、β、θ的含義不是表示小於篩孔尺寸粒級的含量，而是表示要計算級別的物料的含量。
部分篩分效率與總篩分效率關係很大。細粒級的部分篩分效率總是大於總篩分效率，且級別愈細，部分篩分效率愈高；難篩顆粒的部分篩分效率總是小於總篩分效率，並且難篩顆粒尺寸愈接近篩孔尺寸，其部分篩分效率愈低。
分級
所謂分級，就是根據顆粒在流體介質中沉降速度的差異，將物料分成不同粒級的過程。按照所使用的介質，可分為風力分級（乾式分級）和水力分級（濕式分級）兩種；按照沉降方式，可分為重力沉降分級和離心力沉降分級。常用的分級設備有機械分級機、水力分級機、水力旋流器等。
由於分級是按顆粒的沉降速度差異實現分離，因此顆粒的尺寸、形狀、密度及沉降條件等對其分離的精確性均有影響。
按沉降規律進行粒度分離的設備，計算其分級效率有許多標準，如量效率、質效率、總效率、修正效率、折算效率等。下面先介紹量效率、質效率和總效率的概念，至於修正效率和折算效率將在討論水力旋流器數學模型時論述。
如下圖所示，設分級給料、溢流、底流（或沉砂）的固體料量（t/h）分別為Q、Q、Q，其中小於某粒度級別的產率分別為：α、β、θ，則大於某級別的產率分別為α=100-α；β=100-β；θ=100-θ。
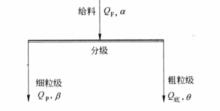分級流程分級量效率。分級的目的是在指定的粒度下，使細、粗顆粒分別進入溢流和底流（或沉砂）。因此可以考慮兩個方面，即細級別進入溢流和粗級別進入底流的回收率，二者愈高愈好，此二指標可分別用其量效率來評價。
細級別存溢流的回收率，即細級別存溢流的量效率E為：
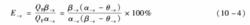量效率E-χ粗級別在底流中的回收率，即粗級別在底流中的量效率Eˊ為：
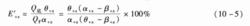量效率Eˊ+χ由式（10-4）很容易算出細顆粒在底流中的回收率Eˊ=100一E。；由式（10—5）很容易算出粗顆粒在溢流中的回收率E=100一Eˊ。很顯然，細顆粒在溢流中的回收率高、粗顆粒在溢流中的回收率低時，分級設備的作業效率才真實反映出來，這就需要用分級質效率來計算。
粒度分離的理論基礎
1.引言
套用篩分和分級對粉碎顆粒實現分離，篩分是按顆粒的大小和形狀進行分離，分級則是按顆粒大小、形狀和密度的差異進行分離；所以如此，是因為上述性質共同影響顆粒在流體介質中的運動。
2.使用水力分級的粒度分離
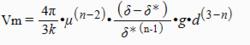臨界速度計算公式流體中的顆粒運動。顆粒在靜止或流動的流體（液體、空氣或氣體）中沉降，大小、形狀和比重不同的顆粒群被分離成性質更為均一的許多組份。由於不同物理性質的顆粒在介質中具有不同的移動速度，因此產生分離現象。在重力影響下，顆粒在液體中沉降，同時遇到一個阻力。當該阻力等於顆粒的有效重量時，顆粒達到恆定的最大沉降速度，通常稱之為臨界沉降速度。對球體而言，此臨界速度（V）可由下式算出：
式中μ一流體的粘度；δ一固體的密度；δ*一流體的密度，g一重力加速度；d一球體的半徑，n和k一顆粒半徑的函式。可將思托克斯和牛頓定律看作是上圖方程式的特例：
思托克斯定律：
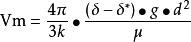粒度分離該定律是當n=l和k=6時，用於小固體顆粒（比如說半徑達0.005厘米的石英球）在水中的降落，這時移動速度低且為層流或粘滯流動（即流線平滑且連續）。
牛頓定律：
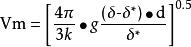粒度分離這個定律是當n=2和k=（π/2） ·Q（Q為阻力係數）時，用於大固體顆粒（如石英顆粒的半徑大於0.25厘米）在水中降落，這時移動速度高為紊流。環繞固體顆粒的液體流線型流動僅限於雷諾數Re=（Vdδ/μ）小於1的條件，如果Re大於2000時，流動則為全紊流。在礦物處理中，最為適用的是層流和紊流之間的範圍，但是這些條件的理論沒有充分加以研究。
在理想情況下，可以利用上面三個方程來預測流體中顆粒的運動，並適當地加以修正以考慮某些因素，例如考慮：（1）顆粒的形狀不規則；（2）其它顆粒干擾該顆粒的降落以及分離容器器壁影響顆粒的降落。
但在實踐中，不能很準確地確定這些因素，而且所遇到的流動方式是如此複雜，以致這些方程不能用於工業迴路的分析和模擬。因此必須使用另外的模擬方法。
