概念
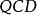 BRST對稱性
BRST對稱性滿足量子化要求的協變規範下的 拉氏量,由於存在規範固定項和鬼場項而丟失了定域規範不變性。即拉氏量在通常的無窮小規範變換
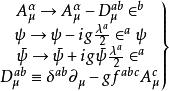 BRST對稱性
BRST對稱性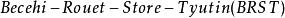 BRST對稱性
BRST對稱性下不是不變的。 指出,如果令
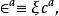 BRST對稱性
BRST對稱性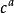 BRST對稱性
BRST對稱性 BRST對稱性
BRST對稱性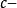 BRST對稱性
BRST對稱性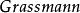 BRST對稱性
BRST對稱性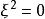 BRST對稱性
BRST對稱性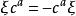 BRST對稱性
BRST對稱性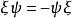 BRST對稱性
BRST對稱性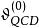 BRST對稱性
BRST對稱性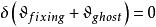 BRST對稱性
BRST對稱性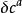 BRST對稱性
BRST對稱性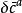 BRST對稱性
BRST對稱性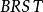 BRST對稱性
BRST對稱性這裡 是鬼場, 是反對易的 數,滿足 代數, , , 等。在上述變換下,原始拉氏量 是不變的,要求 則給出了 、 變換關係,這樣得到如下一組場量的無窮小 變換:
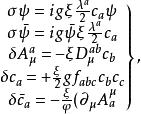 BRST對稱性
BRST對稱性 BRST對稱性
BRST對稱性 BRST對稱性
BRST對稱性 BRST對稱性
BRST對稱性 BRST對稱性
BRST對稱性拉氏量在 變換下不變,稱為 拉氏量的 對稱性。
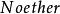 BRST對稱性
BRST對稱性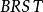 BRST對稱性
BRST對稱性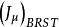 BRST對稱性
BRST對稱性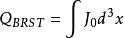 BRST對稱性
BRST對稱性利用 方法,我們可以導出對應於 變換的流 ,相應的荷為 ,則滿足條件
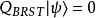 BRST對稱性
BRST對稱性的狀態是體系的物理態。這是協變規範下引入非物理鬼場來消除膠子自作用產生的非物理態的另一種描述。
聯繫BRST對稱性的橫向對稱性變換
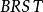 BRST對稱性
BRST對稱性按橫向對稱性變換的定義,我們可寫出與 對稱性相應的橫向對稱性變換為:
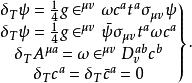 BRST對稱性
BRST對稱性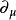 BRST對稱性
BRST對稱性在得到橫向對稱性變換式時,我們將具有矢量特性的“”看做是與矢量場相平等的矢量。如果限制無限小洛侖茲變換運算僅作用在場量上,則我們得到另一組橫向對稱性變換:
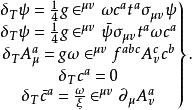 BRST對稱性
BRST對稱性 BRST對稱性
BRST對稱性這兩組變換形式上有所不同,但它們導出的橫向 關係的結果相同。

