AA樹

簡介

AA樹（AA-Tree）是計算機科學中數據結構的一種，屬於自平衡二叉查找樹（Self-balancing binary search tree），是紅黑樹的變種。AA樹是Arne Andersson教授在1993年在他的論文"Balanced search trees made simple"中介紹，設計的目的是減少紅黑樹考慮的不同情況。區別於紅黑樹的是，AA樹的紅結點只能作為右葉子。另外AA樹為實現方便，不再使用紅黑兩種顏色，而是用level標記結點，結點中的level相當於紅黑樹中結點的黑高度。AA樹可以在O(log n)的時間內做查找，插入和刪除，這裡的n是樹中元素的數目。

性能分析

從實現角度看，AA樹減少了紅黑樹插入刪除考慮的情況
AA樹屬於紅黑樹，時間複雜度和紅黑樹相同，即O(logn)，但是鏇轉次數相對較多;

level算法

level的規定滿足以下5個條件
1、每個葉子的level是1
2、每個左孩子的level是其父結點的level減1
3、每個右孩子的level等於其父結點的level或等於其父結點的level減1
4、每個右孫子的level一定比其祖父的level小
5、每個level大於1的結點有兩個孩子

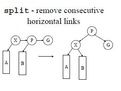
平衡鏇轉

左鏇

出現連續向右的水平方向鏈（連續三個向右的孩子屬於同一level）向左鏇轉：把小於等於此level的結點看做一個子樹

子樹的根的右孩子變為新的子樹根

原來的子樹根變為新子樹根的左孩子

新的子樹根level+1

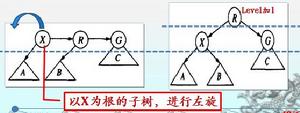
右鏇

出現連續向右的水平方向鏈（連續兩個向左的孩子屬於同一level）
向右鏇轉：
把小於等於此level的結點看做一個子樹

子樹的根的左孩子變為新的子樹根

原來的子樹根變為新子樹根的右孩子

插入結點

插入結點方法和二叉查找樹相同，每次插入值都需要檢查是否需要進行平衡鏇轉。每當出現連續的水平方向鏈，就進行平衡鏇轉。
注意：插入結點時level等於其父結點的level，只有當樹進行鏇轉操作時才會改變結點的level值。

刪除結點

刪除結點按後繼結點右孩子的值賦給後繼結點。
情況1：
如果後繼結點不是葉子，後繼結點右孩子的值賦給後繼結點，最後刪除後繼的右孩子。
情況2：
如果後繼結點是葉子，後繼結點父親的level減1，如果出現向左或連續向右的水平鏈，進行右鏇或者左鏇，最後刪除後繼結點。

Java代碼

在java中定義AA樹的方法public class AATree {　 public AATree( ) {　 root = nullNode;　 } public void insert( Comparable x ) { 　root = insert( x, root );　 } public void remove( Comparable x ) {　 deletedNode = nullNode; root = remove( x, root );　}　public Comparable find( Comparable x ) {　 AANode current = root; 　nullNode.element = x; 　for( ; ; ) {　 if( x.compareTo( current.element ) < 0 )　 current = current.left;　 else if( x.compareTo( current.element ) > 0 )　 current = current.right;　 else if( current != nullNode ) return current.element; 　else return null; } }}