原理
點渦屬於平面流,無限長直線渦管元(見渦旋)在與其垂直的平面中表現為一個點渦。考慮孤立點渦對周圍無界的無粘性不可壓縮流體所誘導的速度場。在流動平面上取極坐標( r,φ),原點放置在點渦處。點渦的強度為 Γ。根據對稱性可知點渦所誘導的速度只有 φ方向的分量 v,且 v= v( r)。對以坐標原點O為心,r為半徑的圓,用聯繫速度環量和渦通量的斯托克斯公式得 v=Γ/2πr。由此可見,速度與半徑成反比,在點渦處趨於無限大,所以點渦本身是流場中的一個奇點。由於點渦外的流動處處無旋且流動為軸對稱,因此存在著速度勢Φ和流函式Ψ,它們和速度之間存在關係:
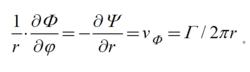 點渦
點渦積分後得到的公式以及與之對應的復變解析函式的表達式為
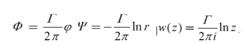 點渦
點渦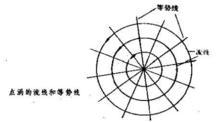 點渦
點渦式中z為復變數;w(z)稱為復位勢。根據Φ和Ψ的表達式易見流線是以點渦為心的同心圓族,等勢線是發自原點的射線族(見圖)。 Γ>0對應於逆時針方向旋轉的點渦; Γ<0對應於順時針方向旋轉的點渦。
套用
龍捲風是點渦的一個例子。在龍捲風的中心附近,流動速度很高,壓力很低。
在平面無旋流動中,點渦是一個重要的基本流,它和均勻流、源流、偶極子流等基本流聯合使用常能得到很多有實際背景的流動。比如,將軸線某線段上的點渦連續分布、點源連續分布和均勻流疊加可得薄翼繞流問題的解。一般說來,對於運動物體所受舉力的問題,在使用奇點分布法求繞流問題的解時,常需採用點渦這種形式的基本流,因為舉力同速度環量有著密切的關係。
在粘性不可壓縮流體中有一類特殊流動,其速度分布同點渦所誘導的速度分布完全相同。當一半徑為 r的直圓柱體在粘性不可壓縮流體中繞圓柱軸線旋轉時,圓柱壁面上的切向速度為 v,令 Γ=2π r。由於粘性的作用,圓柱的旋轉將帶動不同半徑上的流體繞軸旋轉,其速度分布為 v=Γ/2πr,即速度值隨半徑 r的增加成反比地減小。令圓柱半徑趨於零,同時要求 Γ保持一常數值,結果得到一根半徑無限小的剛性柱體在粘性流體中的運動,它所產生的流場和點渦所誘導的完全等同。
參考文獻
1.詞條作者:吳望一 《中國大百科全書》74卷(第二版)物理學 詞條:流體力學 :中國大百科全書出版社 2009-07 :101頁
