渦度
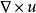 渦矢量
渦矢量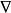 渦矢量
渦矢量渦流動力學中的一個關鍵概念是渦度,一種描述流體中某一點的局部旋轉運動的矢量,如同觀察者一樣可以觀察到的。從概念上講,可以通過將微小的粗球放在有問題的地方,隨著流體自由移動,並觀察其繞其中心旋轉的方式,觀察渦度。渦度矢量的方向被定義為這個假想球的旋轉軸的方向(根據右邊的規則),而它的大小是球的角速度的兩倍。在數學上,渦度定義為流體速度場的捲曲(或旋轉),通常由omega表示,並由矢量分析表示公式表示,其中是nabla運算元和u是本地流速。
由渦度omega測量的局部旋轉不能與流體相對於外部環境的角速度矢量混淆,或任何固定軸。在渦流中,特別地,omega可能與流體相對於渦旋軸的平均角速度矢量相反。
渦矢量的類型
在理論上,渦矢量中顆粒的速度u(以及得到的渦度)可以隨軸的距離r以許多方式而變化。 但有兩個重要的特殊情況:
如果流體像剛體那樣旋轉 - 也就是說,如果角速度Ω是均勻的,使得u與軸線的距離r成比例地增加 - 流動所攜帶的小球也將圍繞其中心旋轉,如同它 是剛體的一部分。 在這樣的流程中,渦度在任何地方是相同的:其方向平行於旋轉軸線,其幅度等於圍繞旋轉中心的流體的均勻角速度ω的兩倍。
如果粒子速度u與軸線的距離r成反比,那么虛擬測試球不會自動旋轉; 當圍繞渦流軸線移動一圈時,它將保持相同的取向。 在這種情況下,渦流omega在任何不在該軸上的點都為零,流動被認為是非旋轉的。
無旋渦
在沒有外力的情況下,渦流通常會相對快速地向非旋轉流動模式演化,其中流速u與距離r成反比。無旋渦也稱為自由旋渦。
對於無旋渦,沿著不包圍渦流軸線的任何封閉輪廓,循環為零;並且具有固定值Γ,對於確定包含軸一次的任何輪廓。粒子速度的切向分量為u _ θ = Gamma\2 \ pi r。因此,相對於渦流軸的每單位質量的角動量是恆定的。
然而,理想的非旋轉渦流不能在物理上可實現,因為這將意味著粒子速度(以及因此保持顆粒在其圓形路徑中所需的力)隨著接近渦流軸線而無限制地增長。實際上,在真實旋渦中,總有一個圍繞軸的核心區域,其中粒子速度停止增加,然後隨著r變為零,減小到零。在該區域內,流動不再是非旋轉的:渦度omega變為非零,方向大致平行於渦旋軸。蘭金渦是一種假定剛體旋轉流的模型,其中r小於固定距離r0,並且在該核心區域之外的非旋轉流動。 Lamb-Oseen渦流模型是Navier-Stokes方程的精確解決方案,它控制流體流動並呈現圓柱形對稱性。
旋轉渦
旋轉渦流 - 離開中心的非零渦度的旋渦- 可以在這種狀態下被無限期地保持在這種狀態,只有通過施加一些額外的力,這不是由流體運動本身產生的。
例如,如果水桶圍繞其垂直軸以恆定角速度ω旋轉,則水將最終以剛體方式旋轉。 顆粒然後沿著圓移動,速度u等於wr 在這種情況下,水的自由表面將呈拋物線形狀。
在這種情況下,剛性旋轉外殼提供額外的力,即水中的額外的壓力梯度,向內引導,從而防止剛體流向非旋轉狀態的演變。
渦旋幾何
在靜止渦流中,典型的流線(與流速矢量相切的線)是圍繞軸線的閉環;並且每個渦旋線(與渦度矢量相切的線)大致平行於軸線。與流速和渦度相切的任何一個表面稱為渦流管。通常,渦流管圍繞旋轉軸線嵌套。軸本身是渦流線之一,渦流管的直徑為零的極限情況。
根據亥姆霍茲定理,渦流不能在流體中開始或結束,除非瞬間,在非穩定流動中,渦流形成或消散。一般來說,渦流線(特別是軸線)是閉環或在流體的邊界處結束。漩渦是後者的一個例子,即在水體中的渦流,其軸在自由表面終止。渦旋管全部關閉的渦流管將是一個封閉的圓環面。
新產生的渦流將迅速延伸和彎曲,以消除任何開放式渦旋線。例如,當飛機發動機起動時,渦流通常在每個噴氣發動機的每個螺旋槳或渦輪風扇前面形成。渦流線的一端連線到發動機,而另一端通常伸出並彎曲直到其到達地面。
 C-17使用大功率引擎工作時產生的渦流中心
C-17使用大功率引擎工作時產生的渦流中心當渦流由煙或墨跡可見時,它們似乎具有螺旋線路或流線。然而,這種外觀通常是幻覺,流體顆粒在封閉的路徑中移動。被認為是流線型的螺旋條紋實際上是標記液的雲,其原始跨越多個渦流管並且通過不均勻的流速分布被拉伸成螺旋形狀。

