概念
麥基空間(Mackey space)是一類局部凸空間。設(X,Y)為對偶線性空間,在Y的每個弱緊凸集上一致收斂的拓撲是一種可允許拓撲,稱為X上的麥基拓撲,記為τ(X,Y)。X上一個局部凸拓撲成為相容拓撲的充分必要條件是它比弱拓撲σ(X,Y)強,而比τ(X,Y)弱。麥基拓撲是最強的相容拓撲。原來的拓撲與麥基拓撲τ(E,E′)相同的局部凸空間E稱為麥基空間。擬桶型空間是麥基空間。
拓撲線性空間
拓撲線性空間是泛函分析的重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的線性空間,是賦范線性空間概念的推廣。
20世紀初,法國數學家弗雷歇在引入距離空間,並用距離概念來統一過去分析學中的許多重要收斂時,就知道[a,b]上一列函式的“點點收斂”概念是不能用距離收斂來描述的。20世紀30年代以來,泛函分析中大量套用弱收斂、弱拓撲,它們都不能用距離來描述。這就很自然地把賦范線性空間理論發展成更一般的拓撲線性空間理論,其中最主要的成就是局部凸拓撲線性空間理論。這一分支的發展是與一般拓撲學的發展緊密聯繫在一起的。拓撲學方法在這裡發揮了極其重要的作用,法國數學家勒雷和波蘭數學家紹德爾所推廣的不動點定理就是有力的例證之一。1935年以後,經過十多年的努力,這一分支終於形成,它的許多結果不僅在泛函分析中有著廣泛的套用,而且為其他分析學科的深入研究提供了基本框架和有力的工具。
局部凸空間
局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間,如果E中存在由均衡凸集組成的零元的鄰域基,就稱E是局部凸的拓撲線性空間,簡稱局部凸空間,而E的拓撲稱為局部凸拓撲。零元的每個均衡凸鄰域V的閔科夫斯基泛函p(x)是E上的連續半範數。反之,設{p|λ∈Λ}是E上一族半範數,E上使p(λ∈Λ)均為連續的最弱拓撲是局部凸的,且零元的均衡凸鄰域基由下面形式的集組成:
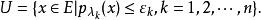 麥基空間
麥基空間這個局部凸拓撲稱為由半範數族{p}確定的局部凸拓撲。如果對任何x∈E(x≠0),都存在λ∈Λ使p(x)≠0,則{p|λ∈Λ}確定的局部凸拓撲是豪斯多夫拓撲。通常局部凸空間都指豪斯多夫局部凸空間。E中的定向半序點列{x}收斂於x∈E等價於對每個λ∈Λ,p(x-x)→0。設E是由另一半範數族{q}確定的局部凸空間,則使線性映射T:E→E連續的充分必要條件是,對任意的q,總存在有限個λ,λ,…,λ∈Λ和常數c,使不等式
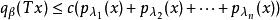 麥基空間
麥基空間對一切x∈E成立。
局部凸空間的完備化空間也是局部凸的。根據哈恩-巴拿赫泛函延拓定理,局部凸空間上存在足夠多的非零連續線性泛函。正因為如此,局部凸空間理論成為拓撲線性空間理論中最重要的部分。
關於局部凸空間理論的發展大約是始於迪厄多內(Dieudonné,J.)和施瓦茲(Schwarz,L.)在1949年的工作,它的一個主要推動力是分布理論,即廣義函式理論。
線性空間的對偶
滿足一定條件的一對線性空間。同一數域K(實數域或複數域)上的線性空間X,Y,如果由X×Y到K的雙線性泛函〈·,·〉滿足下述分離公理:
1.若對每個y∈Y,滿足〈x,y〉=0,則x=0;
2.若對每個x∈X,滿足〈x,y〉=0,則y=0;
那么X和Y稱為互為對偶的線性空間。亦稱Y(或X)是X(或Y)的對偶。
設X是線性空間,X是X上的線性泛函全體,如果Y⊂X,且Y在X上是全的(即若x≠0,則必存在y∈Y使〈x,y〉=y(x)≠0),則(X,Y)按雙線性泛函〈x,y〉=y(x)成為對偶,實際上任何對偶線性空間(X,Y)總可以表達為上述形式。如果E是局部凸空間,E′(或E)是E上的連續線性泛函全體,則(E,E′)稱為自然對偶。線上性空間的對偶概念基礎上所形成的對偶理論是局部凸空間理論的中心內容,它也是把局部凸空間和它的共軛空間放在相對稱的地位來加以研究的。
可允許拓撲
可允許拓撲是一種局部凸拓撲。設(X,Y)是對偶線性空間,Y是Y中的有界集族,且並∪{A|A∈Y}的線性包是Y,即Y是∪{A|A∈Y}張成的線性空間,對每個A∈Y,定義半範數:
p(x)=sup |〈x,y〉|,
則由半範數族{p(x)|A∈Y}確定的X上局部凸拓撲T稱為關於對偶線性空間(X,Y)的一個可允許拓撲,或在集類Y上的一致收斂拓撲,而相應的有界集族Y稱為可允許集族。令F是Y中有限集全體形成的集族,則有T=σ(X,Y),因而弱拓撲是可允許的。
