簡介
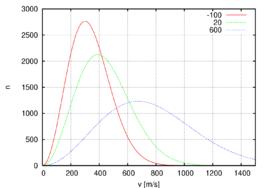
麥克斯韋-玻爾茲曼分布是一個描述一定溫度下微觀粒子運動速度的機率分布，在物理學和化學中有套用。最常見的套用是統計力學的領域。任何（巨觀）物理系統的溫度都是組成該系統的分子和原子的運動的結果。這些粒子有一個不同速度的範圍，而任何單個粒子的速度都因與其它粒子的碰撞而不斷變化。然而，對於大量粒子來說，處於一個特定的速度範圍的粒子所占的比例卻幾乎不變，如果系統處於或接近處於平衡。麥克斯韋-玻爾茲曼分布具體說明了這個比例，對於任何速度範圍，作為系統的溫度的函式。它以詹姆斯·麥克斯韋和路德維希·玻爾茲曼命名。
麥克斯韋-玻爾茲曼分布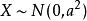
麥克斯韋-玻爾茲曼分布這個分布可以視為一個三維矢量的大小，它的分量是獨立和常態分配的，其期望值為0，標準差為a。如果的分布為，那么
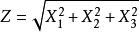麥克斯韋-玻爾茲曼分布就呈麥克斯韋-玻爾茲曼分布，其參數為a。
麥克斯韋-玻爾茲曼分布的物理套用
麥克斯韋-玻爾茲曼分布形成了分子運動論的基礎，它解釋了許多基本的氣體性質，包括壓強和擴散。麥克斯韋-玻爾茲曼分布通常指氣體中分子的速率的分布，但它還可以指分子的速度、動量，以及動量的大小的分布，每一個都有不同的機率分布函式，而它們都是聯繫在一起的。
麥克斯韋-玻爾茲曼分布可以用統計力學來推導（參見麥克斯韋-玻爾茲曼統計）。它對應於由大量不相互作用的粒子所組成、以碰撞為主的系統中最有可能的速率分布，其中量子效應可以忽略。由於氣體中分子的相互作用一般都是相當小的，因此麥克斯韋-玻爾茲曼分布提供了氣體狀態的非常好的近似。
在許多情況下（例如非彈性碰撞），這些條件不適用。例如，在電離層和空間電漿的物理學中，特別對電子而言，重組和碰撞激發（也就是輻射過程）是重要的。如果在這個情況下套用麥克斯韋-玻爾茲曼分布，就會得到錯誤的結果。另外一個不適用麥克斯韋-玻爾茲曼分布的情況，就是當氣體的量子熱波長與粒子之間的距離相比不夠小時，由於有顯著的量子效應也不能使用麥克斯韋-玻爾茲曼分布。另外，由於它是基於非相對論的假設，因此麥克斯韋-玻爾茲曼分布不能做出分子的速度大於光速的機率為零的預言。
參見
•玻爾茲曼因子
•瑞利分布
•理想氣體狀態方程
•詹姆斯·克拉克·麥克斯韋
•分子運動論
