定義
當溫度一定時,氣體分子速率平方的平均值是一定的。在任何一瞬間,分子的速率大小可能有許多值:有些分子速率為零;而同時又有一些分子的速率比平均速率大得多。究竟某一速率內的分子有多少個,另一速率內的分子又有多少個,可由分子速率分布來說明。當分子數目很大時,速率的分布必然服從一定的統計規律,即速率分布定律。首先由麥克斯韋從理論推出其公式,氣體分子速率分布定律的公式,稱為麥克斯韋速率分布定律。
歷史
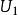 麥克斯韋速度分布定律
麥克斯韋速度分布定律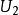 麥克斯韋速度分布定律
麥克斯韋速度分布定律1859年,J.C.麥克斯韋首先獲得氣體分子速度的分布規律,爾後,又為L.玻耳茲曼由碰撞理論嚴格導出。處於平衡狀態下的理想氣體分子以不同的速度運動,由於碰撞,每個分子的速度都不斷地改變,使分子具有各種速度。因為分子數目很大,分子速度的大小和方向是無規的,所以無法知道具有確定速度U的分子數是多少,但可知道速度在與之間的分子數是多少。它表明:氣體在巨觀上達到平衡時,雖然個別分子的速度一般都不相同,並且由於相互碰撞而不斷發生變化,但平均來說,速度在某一範圍內的分子數在總分子數中所占的百分比總是一定的;該比值只與氣體的種類及溫度有關。
函式式的推導
通過玻爾茲曼能量分布定律,我們很容易導出了分子按速度分布的函式式來,因為分子的動能與其速度之間有如下的關係:
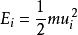 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-1)
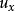 麥克斯韋速度分布定律
麥克斯韋速度分布定律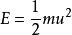 麥克斯韋速度分布定律
麥克斯韋速度分布定律首先考慮分子在一維空間內沿x方向運動的速度分布情況:設分子的質量為m,它在x方向上的速度分量為,現將代入得:
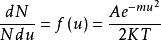 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-2)
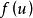 麥克斯韋速度分布定律
麥克斯韋速度分布定律上式即為速度分布函式的表達式,速度分布函式又稱為幾率密度。
如果將上式在全部速度範圍內進行積分,套用歸一化條件(即分子在全部速度範圍內出現的幾率總和應等於1),便可求得上式中的常數A。歸一化條件表示如下:
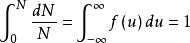 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-3)
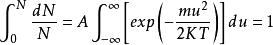 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-4)
運用以下的標準積分結果:
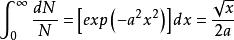 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-5)
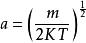 麥克斯韋速度分布定律
麥克斯韋速度分布定律其中可得(1-4)式的解:
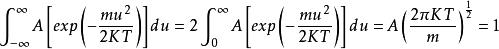 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-6)
所以
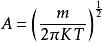 麥克斯韋速度分布定律
麥克斯韋速度分布定律將A值代入(1-2)式中,即得速度分布函式如下:
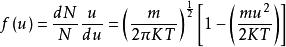 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-7)
 麥克斯韋速度分布定律
麥克斯韋速度分布定律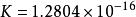 麥克斯韋速度分布定律
麥克斯韋速度分布定律上式稱為Maxwell-Boltzmann速度分布定律,式中的T為絕對溫度,K為玻爾茲曼常數(爾格/度)。
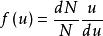 麥克斯韋速度分布定律
麥克斯韋速度分布定律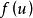 麥克斯韋速度分布定律
麥克斯韋速度分布定律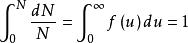 麥克斯韋速度分布定律
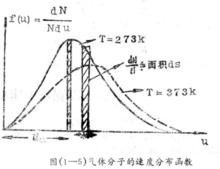
麥克斯韋速度分布定律下面我們用圖形來說明速度分布函式的幾何意義:以和u作圖,得到右圖1所示的曲線,函式表示該曲線的方程式,曲線下方的窄長陰影面積,表示在速度u的附近的單位區間內出現的分子數(dN)占總分子數N的百分率,曲線覆蓋的總面積表示分子所占的百分率之總和,該總和應等於1(因為)。
 麥克斯韋速度分布定律
麥克斯韋速度分布定律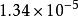 麥克斯韋速度分布定律
麥克斯韋速度分布定律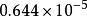 麥克斯韋速度分布定律
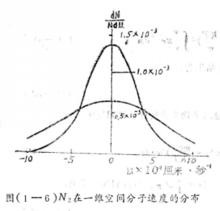
麥克斯韋速度分布定律例如氮氣分子(分子量為28)在一維空間內運動的分布函式,表示在右圖2中,在25℃和在1025℃兩種溫度下,A值分別為秒/厘米和秒/厘米。由於分子運動正向和反向的機會相等,曲線呈對稱形狀,其最可幾速率為零。
速度分布函式
二維相與三維相的速度分布函式
在二維空間內分子按速度分布的規律,依上述方法可求得速度分布函式如下:
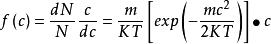 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-8)
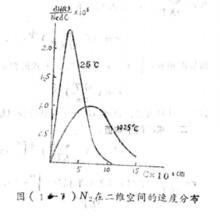
式中的c表示分子在x、y兩個方向上的速度分量u和v的組合。當u和v的增量為du和dv時,淨速度c由增至c+dc。氮分子在x、y兩個方向上的速度分布曲線如圖3所示。
在三維空間內所得的分子速度分布定律表示如下:
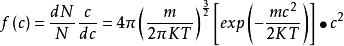 麥克斯韋速度分布定律
麥克斯韋速度分布定律(1-9)
式中的c表示分子在x、y、z三個方向上的速度分量u、v、w的組合。當u、v、w獲得增量du、dv、dw時,速度c相應的由c增加至c+dc。
 麥克斯韋速度分布定律
麥克斯韋速度分布定律 麥克斯韋速度分布定律
麥克斯韋速度分布定律右圖3中的分布曲線,其兩端幾近於橫軸並具有一個極大點,這表明速度最大和最小的分子數目較少,而具有中等速度的分子占總分子數的分數為最大。與曲線的極大點相對應的速度即為最可幾速度,用符號來表示。分布函式f(c)與溫度和速度的數值有關,我們比較圖中的兩條曲線可以看出:當溫度升高時,曲線的峰值降低並向高速方向移動,這意味著在分子總數目不變的情況下,具有較大速度的分子所占的分數,隨溫度的升高而增大,由於分布函式與速度呈負指數關係,當速度增大時,速度大的分子所占的分數迅速的下降,但在給定速度下的分子出現幾率,具有確定不變的數值。
