定義
 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線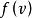 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線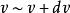 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線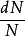 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線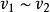 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線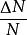 麥克斯韋速率分布曲線
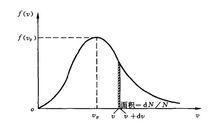
麥克斯韋速率分布曲線以 為橫軸,以麥克斯韋分布函式 為縱軸,畫出的圖線叫做麥克斯韋速率分布曲線(如圖所示),它能形象地表示出氣體分子按速率分布的情況。圖中任一區間 內曲線下的窄條面積表示在該區間內的分子數占總分子數的比率 ,而任一有限範圍 內曲線下的面積則表示分布在這範圍內的分子所占的比率
 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線曲線分析
 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線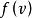 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線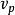 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線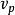 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線由上圖可見速率分布曲線從坐標原點出發,經過一極大值後,隨速率的增大而漸近於橫坐標軸。這說明,氣體分子的速率可以取由0到 之間的一切數值,速率很大和很小的分子所占的比率實際上都很小,而具有中等速率的分子所占的比率卻很大。與 極大值對應的速率叫做最概然速率,通常用 表示。它的物理意義是,如果把整個速率範圍分成許多相等的小區間,則分布在 所在的區間的分子比率最大。於是有
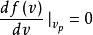 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線由此得
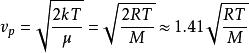 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線(1)
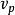 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線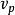 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線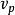 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線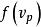 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線即溫度越高, 越大;分子質量越大, 越小。與 對應的 值為
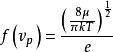 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線(2)
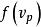 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線即溫度越高, 值越小。
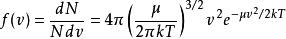 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線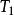 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線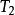 麥克斯韋速率分布曲線
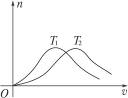
麥克斯韋速率分布曲線麥克斯韋分布函式 表明,對於給定的氣體(即 一定),分布曲線的形狀隨溫度而變。如右圖中畫出了 和 兩個溫度的分布曲線。當溫度升高時,速率較大的分子加多,
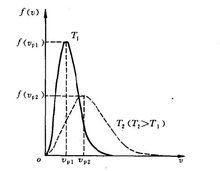 溫度不同的速率分布曲線
溫度不同的速率分布曲線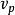 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線最概然速率 變大,所以曲線的高峰移向速率大的一方。但由於曲線下的總面積恆等於1,所以溫度升高時曲線變得較為平坦。
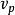 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線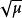 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線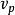 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線在同一溫度下,分布曲線因氣體不同而異。因為最概然速率 與分子質量的平方根 成反比,所以大質量分子的 小,曲線高峰移向速率小的一方。
用麥克斯韋速率分布函式可以求出平衡態下理想氣體分子的平均速率。平均速率的定義是
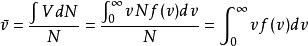 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線將麥克斯韋速率分布函式代入上式,可得
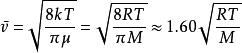 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線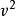 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線還可以用速率分布函式求 的平均值。由平均值的定義有
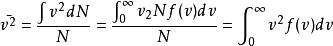 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線將麥克斯韋分布函式代入求解後,並取平方根,可得方均根速率為
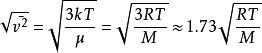 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線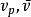 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線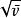 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線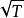 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線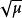 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線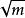 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線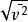 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線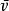 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線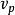 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線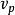 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線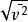 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線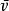 麥克斯韋速率分布曲線
麥克斯韋速率分布曲線由上面的結果可見,氣體分子的3種統計平均速率值 和 都與 成正比,與 或 成反比。其中 最大, 次之, 最小。在室溫下,它們的數量級一般為每秒幾百米。3種速率有不同的套用,討論速率分布時要用到最概然速率 ;在計算分子的平均平動動能時要用到方均根速率 ;以後在計算分子的碰撞頻率時,要用到平均速率 。