簡介
鮑威爾法，嚴格來說是鮑威爾共軛方向法，是麥可J.D.鮑威爾提出的一種求解函式局部最小值的算法。該函式不能是可微分的，並且不會導出衍生函式。
該函式必須是固定數量的實值輸入的實值函式。通過傳入一組初始搜尋向量，通常會傳入N個搜尋向量（譬如{s,,,,,s}）這是與每個軸對齊的法線。
鮑威爾法是在無約束最佳化共扼方向，從某個初始點出發，求目標函式在這些方向上的極小值點，然後以該點為新的出發點，取復這一過程直到獲得滿意解，其優點是不必計算目標函式的 梯度就可以在有限步內找到極值點。
計算過程
鮑威爾法依次通過沿著每個搜尋向量的雙向搜尋使功能最小化。沿著每個搜尋向量的雙向線搜尋可以通過黃金分割搜尋或黑雁的方法來完成。讓每個雙向線搜尋中找到的最小值為
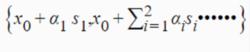鮑威爾法其中x0是起始點，αi是沿著si的雙向搜尋確定的標量。然後可以將新位置（x1）表示為搜尋向量的線性組合，即
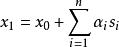鮑威爾法新的位移矢量
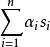鮑威爾法成為新的搜尋向量，並被添加到搜尋向量列表的末尾。
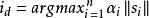鮑威爾法同時，對新方向貢獻最大的搜尋向量，即最成功的搜尋向量（）搜尋向量列表。新的N個搜尋向量集合是
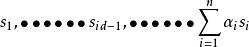鮑威爾法該算法疊代任意次數，直到沒有明顯的改善。
該方法對於計算連續但複雜函式的局部最小值是有用的，特別是沒有基礎數學定義的函式，因為不需要導數。基本算法簡單;複雜度在沿著搜尋向量的線性搜尋中，這可以通過布倫特法來實現。
布倫特法
定義
布倫特方法(the method of Brent)是在二分法或試位法的基礎上，藉助二次插值方法進行加速，有利用反插值方法來簡化計算而形成的一種方法。
內容
假如知道f(x)的零點x’在一個不太大的區間[x0,x1]內，而且已知f(x)在區間的端點處的函式值
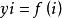鮑威爾法以及f（x）=0在（x0,x1）內的近似解x=x2和f(x2)，接下來利用這已知的三個點以及它們所對應的函式值作插值拋物線。與Muller方法不同的是，把x0 ，x1 ，x2 與f(x0), f(x1), f(x2)的對應關係反過來用，相當於用y0 ，y1 ，y2 替代方程組
f(x0)= a(x0-x2) ^2+b(x0-x2)+c **************** (1)
f(x1)= a(x1-x2) ^2+b(x1-x2)+c **************** (2)
f(x2)= a(x2-x2) ^2+b(x2-x2)+c **************** (3)
中的x0 ，x1 ，x2 ，而方程組的常數項f(x0), f(x1), f(x2) 則用這裡的x0 ，x1 ，x2替換。所以對應的插值拋物線的一般形式為
x= a(y-y2) ^2+b(y-y2)+c **************** (4)
x0= a(y0-y2) ^2+b(y0-y2)+c **************** (5)
x1= a(y1-y2) ^2+b(y1-y2)+c **************** (6)
x2= a(y2-y2) ^2+b(y2-y2)+c **************** (7)
由（5）（6）（7）式可以得c=x2,利用Muller方法，可以寫成a,b 的表達式。
在（4）中令y=0,可以得到下一個近似點為
X=x2+(ay2 ^2+by2) **************** (8)
其中ay2 ^2+by2相當於校正項。
Brent方法的下一個規則是，如果得到的x仍然在區間[x0,x1]內，則用x2根據f(x2)
的符號替換x0或x1 ，用x替換x2；如果所得到的x不在區間[x0,x1]內，則暫時放棄反拋物線插值法，繼續用二分法或試位法。
實際上，我們可以利用二分法所得到函式順便採用反插值方法試探一下。
