簡介
魯棒性
所謂魯棒性，是指控制系統在一定（結構，大小）的參數攝動下，維持某些性能的特性。根據對性能的不同定義，可分為穩定魯棒性和性能魯棒性。以閉環系統的魯棒性作為目標設計得到的固定控制器稱為魯棒控制器。
性能指標的魯棒性分析方法也可分為頻域和時域兩種，使用何種性能指標，要視提出的性能指標是在頻域還是在時域而定。
魯棒控制
魯棒控制（RobustControl）方面的研究始於20世紀50年代。在過去的20年中，魯棒控制一直是國際自控界的研究熱點。魯棒控制的早期研究，主要針對單變數系統（SISO）的在微小攝動下的不確定性，具有代表性的是Zames提出的微分靈敏度分析。然而，實際工業過程中故障導致系統中參數的變化，這種變化是有界攝動而不是無窮小攝動，因此產生了以討論參數在有界攝動下系統性能保持和控制為內容的現代魯棒控制。
實驗中總是假設已經知道了受控對象的模型，但由於實際中存在種種不確定因素，如：
參數變化；
未建模動態特性；
平衡點的變化；
感測器噪聲；
不可預測的干擾輸入
所以所建立的對象模型只能是實際物理系統的不精確的表示。魯棒系統設計的目的就是要在模型不精確和存在其他變化因素的條件下，使系統仍能保持預期的性能。如果模型的變化和模型的不精確不影響系統的穩定性和其它動態性能，這樣的系統就稱它為魯棒控制系統(robust control system)。
魯棒控制理論是分析和處理具有不確定性系統的控制理論，包括兩大類問題：魯棒性分析及魯棒性綜合問題。主要的魯棒控制理論有：
Kharitonov區間理論；
H∞控制理論；
結構奇異值理論（μ理論）；
魯棒調節器設計
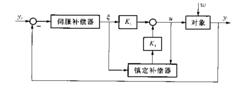魯棒調節器結構框圖Davison提供的魯棒調節器由兩部分組成，一是伺服補償器，二是鎮定補償器。伺服補償器是按設定與擾動作用的變化形式(如階躍變化、斜坡函式變化等)來確定的，以達到無穩態偏差的要求。鎮定補償器的作用是使系統在參數變化條件下仍保持穩定，並有一定裕度。
魯棒調節器的一般形式為：
μ= K1 ξ +K2η
式中K1，K2 為增益矩陣,ξ為伺服補償器輸出,η為鎮定補償器輸出
主要研究
魯棒控制的早期研究，主要針對單變數系統（SISO）的在微小攝動下的不確定性，具有代表性的是Zames提出的微分靈敏度分析。然而，實際工業過程中故障導致系統中參數的變化，這種變化是有界攝動而不是無窮小攝動。因此產生了以討論參數在有界攝動下系統性能保持和控制為內容的現代魯棒控制。
現代魯棒控制是一個著重控制算法可靠性研究的控制器設計方法。其設計目標是找到在實際環境中為保證安全要求控制系統最小必須滿足的要求。一旦設計好這個控制器，它的參數不能改變而且控制性能能夠保證。
魯棒控制方法，是對時間域或頻率域來說，一般要假設過程動態特性的信息和它的變化範圍。一些算法不需要精確的過程模型，但需要一些離線辨識。
一般魯棒控制系統的設計是以一些最差的情況為基礎，因此一般系統並不工作在最優狀態。常用的設計方法有：INA方法，同時鎮定，完整性控制器設計，魯棒控制，魯棒PID控制以及魯棒極點配置，魯棒觀測器等。
魯棒控制方法適用於穩定性和可靠性作為首要目標的套用，同時過程的動態特性已知且不確定因素的變化範圍可以預估。飛機和空間飛行器的控制是這類系統的例子。
過程控制套用中，某些控制系統也可以用魯棒控制方法設計，特別是對那些比較關鍵且（1）不確定因素變化範圍大；（2）穩定裕度小的對象。
圖書但是，魯棒控制系統的設計要由高級專家完成。一旦設計成功，就不需太多的人工干預。另一方面，如果要升級或作重大調整，系統就要重新設計。
最新套用
柔性直流附加魯棒阻尼控制器設計
針對包含柔性直流（VSC-HVDC）的交直流互聯繫統區間低頻振盪現象,提出把基於線性矩陣不等式的多目標控制方法套用到柔性直流附加控制中。具體包括運用最小二乘-旋轉不變方法（TLS-ESPRIT）辨識出系統降階模型,綜合考慮控制器的魯棒性和控制代價,設定多目標函式,設計出H2/H∞多目標魯棒附加阻尼控制器,並設計傳統極點配置控制器進行比較。在PSCAD/EMTDC中搭建包含柔性直流的四機兩域電磁暫態模型,特徵值分析和時域仿真結果表明：在系統內部參數發生較大變化情況下,多目標魯棒阻尼控制器具有更好的阻尼特性,併兼顧了控制器的控制代價。
靜態H∞迴路成形法的多通道魯棒阻尼控制
通過附加魯棒阻尼控制器來同時抑制次同步振盪和低頻振盪，通過求解線性矩陣不等式直接求解出控制器，採用總體最小二乘旋轉不變技術辨識出系統振盪模態及降階模型，利用巴特沃茲帶通濾波器將系統不同振盪模態分解為多個通道，根據靜態H ∞ 迴路成形法針對不同的通道設計魯棒阻尼控制器，降低控制器間相互影響。與傳統的比例‑積分‑微分（PID）控制器相比結果表明，具有更好的控制效果，能同時抑制次同步振盪和低頻振盪，具有較好的魯棒性；同時所設計的控制器階數較低，採用輸出反饋，便於工程實踐，且具有計算量較小，算法複雜度較低等特點。
