控制簡介
傳統的PID控制是誤差的比例、積分、微分三項的線性組合，它具有原理簡單、參數易於調整、魯棒性較強等特點，在工業過程控制中得到了廣泛的套用。但是對於一些複雜的系統，特別是非線性對象，PID控制器並不能得到滿意的效果。如果對傳統的PID加以改進，使其能對一些非線性對象實現較高的控制要求，將有很大的實際意義。非線性PID是在傳統PID的基礎上引進非線性因素來加以改進的，控制量的基本要素不是直接取自輸入-輸出的誤差，而是經過非線性變化後的誤差的比例、積分和微分。由於非線性PID控制器中的增益參數能夠隨控制誤差而變化，從而克服和減弱了非線性因素的影響，提高了控制器的魯棒性和適應性 。
結構原理圖
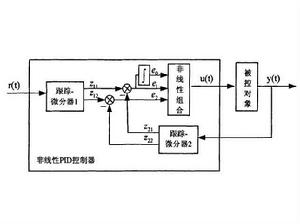
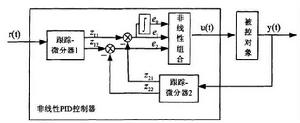圖1 非線性PID控制器的基本結構
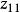非線性PID控制
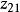非線性PID控制
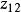非線性PID控制
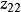非線性PID控制
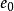非線性PID控制
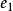非線性PID控制
非線性PID控制圖1是非線性PID控制器的結構原理圖。圖中，r(t) 為 參考輸入信號，u(t)、y(t)分別是受控系統的輸入和輸出信號：非線性跟蹤-微分器1、2的輸出信號中 、 分別跟蹤 r(t) 和y(t)， 、 分別為 r(t)和 y(t) 的微分信號； 、 、 是跟蹤-微分器輸出的參考輸入和系統輸出之間的偏差及其積分和微分變數 。
控制模型
PID控制器可表示為：
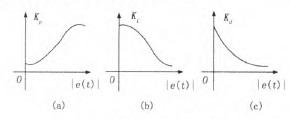圖2 增益參數理想調節變化規律 非線性PID控制式中，Kp(e(t))、Ki(e(t))、Kd(e(t))分別為比例、積分和微分係數，它們都是誤差的非線性函式。根據經典控制原理，系統階躍回響過程中控制器P / I / D各部分的控制作用，相應的增益參數的理想變化如圖2所示。
比例控制Kp
Kp加快回響速度，減少過渡過程時間。為保證系統有足夠的回響速度，Kp的大小應與誤差的絕對值成正比，且當e(t)=0時，應保證Kp為合理的非零值，由此取比例係數的調節律為：
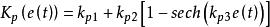非線性PID控制積分控制Ki
Ki減少系統的穩態誤差。當e(t)大時，Ki較大；當e(t)小時，Ki較小。所以積分係數的調節律為：
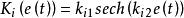非線性PID控制微分控制Kd
Kd增大系統阻尼，降低過渡過程時間。在不影響速度的前提下，Kd應隨e(t)逐漸增大，但同時應限制Kd以抑制超調。由此微分係數的調節律為：
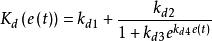非線性PID控制
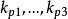非線性PID控制
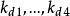非線性PID控制
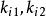非線性PID控制
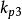非線性PID控制
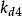非線性PID控制
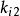非線性PID控制上述3式中， ， ， 都為正實數。通過調整 、 、 的大小分別調整Kp、Kd、Ki的變化速率。按上述PID控制器參數在系統動態過程中的調節規律，即各參數與誤差e(t)之間的非線性函式關係，分別調節控制器各部分的控制作用 。
