定義
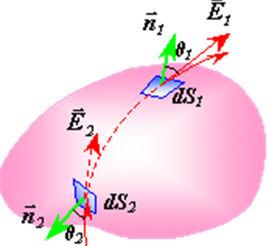
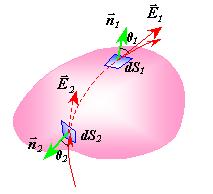 高斯面
高斯面高斯定理是電磁學的基本定理之一,它給出了靜電場中,穿過任一閉合曲面S的電通量與該閉合曲面內包圍的電量之間在數值上的關係。一般的說,高斯定理說明靜電場中電場強度對任一曲面的通量只取決於該閉合曲面內包圍電荷的電量的代數和,與閉合曲面內的電荷分布及閉合曲面外的電量無關。但是應該指出,雖然高斯定理中穿過閉合曲面的電通量只與曲面內包圍的電荷有關,然而定理中涉及的電場強度卻是所有(包括曲面內外)源電荷產生的總電場強度。
計算方法
簡單的說,高斯面的計算就是:矢量穿過任意閉合曲面的通量等於矢量的散度對閉合面所包圍的體積的積分。公式為:
∮EdS=∫▽Edv 。
▽即是哈密頓算符,E、S為矢量。
高斯定理在物理學研究方面,套用非常廣泛。
如:電場E為電荷q(原點處)在真空中產生的靜電場,求原點外M(x,y,z)處的散度divE(M).
解:div(qR/(4πr^3)=0 R/r--為r的單位矢量。
靜電場屬於有源場
套用高斯定理(或散度定理)求靜電場或非靜電場非常方便。特別是求靜電場中的場強,在普通物理學中常用,這裡就再舉二例。
現在用高斯公式推導普通物理中的高斯定理,
設S內有一點電荷Q其電場過面積元dS的通量為
E·dS=Ecosθds
=Q/(4πε0r^2)* cosθds θ為(ds^r) ε0----真空中的介電常數
顯然cosθds為面元投影到以r為半徑的球面的面積,在球體內,面元dS對電荷Q所張的立體角為dΩ= cosθds/r^2
故 E·ds= Q/(4πε0)dΩ
因此,E對閉合曲面S的通量為∮E·dS=Q/(4πε0) ∮dΩ=Q/ε0。