簡介
 食分示意圖
食分示意圖在日食過程中,在地球表面上看到月球的角直徑(Angular diameter)與太陽的角直徑的比例,稱為食分(英語:Magnitude of eclipse)。雖然太陽的實際大小,比月亮的實際大小相差很遠。但是由於月球與地球的距離比太陽的近,因此在地球上,我們可以看到月球與太陽的大小大致相同,但在不同時間都會出現差異。 而在月食過程中,在地球表面上看到地球的本影與月球的角直徑的比例,亦稱為食分。
所以食分是指在一次日食中,月球的角直徑,與太陽角直徑的比例或者指一次月食中,地球本影的角直徑,與月球角直徑的比例。在英語上,食分是Magnitude。但同時,Magnitude亦指星等。因此有人把食分和星等混淆;在定義上:食分是指星體覆蓋的角直徑長度之比,而星等則指星體亮度。
計算公式
現代計算方法
日食的食分反映了月球掩蓋太陽的程度。食分越大,太陽被掩蓋的比例越高。食分的數字可表示該次食的情況。但是不要把食分和被掩蓋面積比例混淆,兩者的定義如下:
日食食分=BC/AB
=太陽被掩蓋的長度(沿太陽和月球中心的連線)/太陽的視直徑
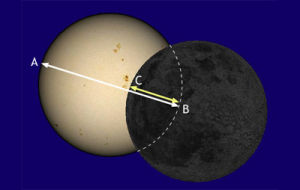 食分示意圖
食分示意圖被掩蓋的面積比例=太陽被掩蓋的面積/太陽的視面積
| 食分 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
| 被掩蓋的面積部分 | 0 | 3.7 | 10.4 | 18.8 | 28.5 | 39.1 | 50.5 | 62.4 | 74.7 | 87.3 | 100 |
食分與被掩蓋面積比例的比較
中國古代計算方法
中國古代的日食食分算法始於北魏張龍祥所造的《正光歷》,《魏書卷一百七·志第八》“推蝕分多少術曰:置入交限十五度,以朔望去交日數減之,余則蝕分。按太陽在黃道上日行一度,《正光歷》實際上給出了如下的食分算法:食分=15一去交度數。”
這是中國古代曆法中出現的第一例日食食分算法,也是中國古代日食食分算法最基本的形式。
按《正光歷》取日食不偏食限為15度,且將日面視直徑等分為15分,上面的公式和下面的公式是等價的:
食分=(15–去交度數)/15*15
影響因素
日食
 食分中的食甚
食分中的食甚月食
月食與日食不相同。日食是指太陽被月球遮蓋而出現的情況,因此地球看到日食。而月食則指月球被地球所遮蓋而出現的情況,月球部分地區沒被太陽完全照射,因此地球看到月食。月食並沒有所謂月環食,這是由於月食時,地球的本影必然比月球大。另外,在不同地區看到的月食情況都是相同的(不包括天氣、角度位置)。食分比例
 食分
食分日食
在一次日食中,若食分等於0的話:表示太陽並沒有被任何星體包括月亮所覆蓋,太陽光度並沒有改變。 食分
食分若食分在0至1之間的話:表示部分太陽被月球覆蓋。若當時地球、月球及太陽成一直線時,則形成一個環的形狀,因此被稱為日環食 ,光度減弱大半,但仍看到影子。若月球只是部分略過太陽,而沒有形成一個環形的話,被稱為日偏食 。而當時,指定地區將會變成較為昏暗,視乎食分多少。
若食分大於1的話,表示太陽被月球完全覆蓋,因此被稱為日全食 。全食帶上的地區因沒有陽光,變得非常昏暗,太陽背景上的星空均可見。
若食分剛好在1左右,則同一次日食中在不同地區可能出現日全食與日環食。這個情況十分罕見,被稱為全環食 。
月食
 食分
食分而在一次月食中,若食分等於0的話:表示月球沒有被任何地球的影子所覆蓋。
若食分介乎0至1之間的話:表示月球被部分地球覆蓋。若當時月球被地球半影覆蓋,即月球只被地球擋住部分太陽光的話,稱為半影月食,若地球本影掠過月球,則被稱為月偏食 。
若食分大於1的話,表示月球被地球的本影完全覆蓋,因此被稱為月全食 。但由於地球的大氣層能折射太陽光,全食時仍能在地球上看到一個偏紅的月球。
其他
 食分
食分每次日食,相關部門例如美國國家航空航天局都會公布日食及月食的食甚。食甚是指一次食中,最大的食分,亦標明地區。例如,在日全食中,最大食的地區之食甚至可以維持少於1秒至7分鐘不等。食甚亦指於指定地區出現日食或月食現象時,食分最大時刻的狀況。
所有日食的過程(括弧中狀況只有日全食才出現):初虧、(食既)、食甚、(生光)、復圓

