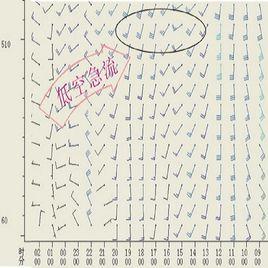
描述及規律
在邊界層,風速隨高度的變化服從普朗特的理論:
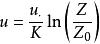 風廓線
風廓線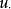 風廓線
風廓線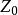 風廓線
風廓線式中u為高度Z上的風速,K為卡曼常數,其值為0.4左右。為摩擦速度, 為粗糙度參數。
若換算成兩個高度的風速關係,則為:
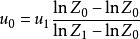 風廓線
風廓線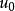 風廓線
風廓線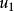 風廓線
風廓線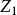 風廓線
風廓線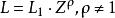 風廓線
風廓線為高度Zn的風速, 為在高度 處的風速。這是中性平衡時風速隨高度變化的對數律公式。在需用速度廓線的許多數學間題中,把對數律公式引進到微分方程中去會發生困難,這時假設混合長度隨高度變化為,則得到風速隨高度變化的乘冪律公式。換成兩個高度的風速關係,用以上同樣方法可導出公式:
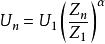 風廓線
風廓線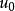 風廓線
風廓線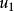 風廓線
風廓線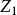 風廓線
風廓線公式中 、 、Zn、 含義同上,α為風速隨高度變化係數,是一個與大氣穩定度和地形條件有關的參數,查表獲得,此式通稱為指數公式。
風廓線形狀
應該指出的是過去的工作中,大氣低層風速廓線無論採用指數公式還是對數公式都還是一個統計規律,即這兩個公式符合於在長期連續觀測取平均值時的風廓線。這種平均風廓線在直角坐標紙上表現為一條風速隨高度而增加的曲線,在對數坐標紙上近似為一條直線或接近於直線。但在各次觀測中的風速廓線並非都象平均風廓線一樣,它可以呈現出各種形狀。
計算方法
弄清近地層平均風速垂直分布的規律對於理論研究和實際套用都十分重要。
對數風廓線
在中性條件下,對數風速廓線能夠很好地描述平均風速隨高度的變化。這個關係已經在100m高度以內的實際觀測得到了證明。在非中性條件下,必須考慮對穩定度的訂正。
複合指數風廓線
在不穩定條件和中性條件下,複合指數風速廓線能夠較好地描述均勻表面上的近地層風速廓線。這個模式在近來的一些文章中被討論到,並且有人用實際觀測數據進行了檢驗。
莫寧一奧布霍夫相似理論
在非中性條件下,套用莫寧一奧布霍夫相似理論也可以解決穩定度訂正的難題,由此建立的通量一廓線關係式已經被成功地套用到近地層風速廓線的描述中。然而,由於必須先通過實驗方法確定其中的相似函式,並預先估計奧布霍夫長度和其它一些參數,這使得該方法在估計風速廓線的實際套用中並不方便。