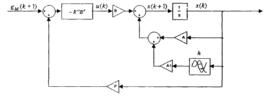
非線性系統
概述
隨著科學技術的不斷發展,人們對實際生產過程的分析要求日益精密,各種較為精確的分析和科學實驗的結果表明,任何一個實際的系統都是非線性的。所謂線性只是對非線性的一種簡化或近似,或者說是非線性的一種特例。雖然許多物理關係常以線性方程表示,但是在大多數情況下,實際的關係並非真正線性的。對物理系統仔細研究後會發現,即使對所謂的線性系統來說,也只是一定工作範圍內保持真正的線性關係。實際上,許多電機械系統、液壓系統和氣動系統等在變數之間都包含著非線性關係。嚴格來說,非線性系統才是最一般的系統。而線性系統只是其中的特殊情況。因而研究非線性系統更能發掘自然界的本質。
近年來非線性科學越來越受到人們的重視,數學中的非線性分析、非線性泛函,物理學中的非線性動力學等,發展得都很迅速。與此同時,非線性理論得到了蓬勃發展。與20年前相比,現在有更多的控制學家轉入非線性系統的研究,更多的工程師力圖用非線性理論設計與控制實際工程系統。這一方面是由於理論的發展,特別是非線性系統幾何理論的誕生,為實際套用提供了可能性;另一方面,則來自實踐的需要,特別是航空、航天等高新技術對精度要求越來越高,使傳統的近似方法無法滿足。
事實上,非線性控制系統的發展幾乎是與線性系統平行的,但非線性系統的理論遠不及線性系統的理論完善。這主要是由於非線性系統本身所包含的現象十分豐富,迄今為止對它的了解還不夠。例如,線性系統的穩定性只有穩定,漸近穩定和不穩定:而非線性系統解的性態要複雜的多,系統的穩定性除了穩定,漸近穩定,不穩定外,它還可能有極限環(穩定極限環和不穩定極限環)以及混沌和分叉等,但對非線性系統合適的數學工具卻遠遠不夠。
非線性控制理論的突破性進展發端於20世紀70年代初期。隨著微分幾何理論和微分代數方法的引入,使得非線性系統控制理論及其套用有了一個巨大飛躍。
特點及優點
先來介紹非線性系統的主要特點:
(l)穩定性
線性系統的穩定性只是取決於系統的結構和參數,而與外作用和初始條件無關。對於非線性系統,則不存在整個系統是否穩定的籠統概念,必須針對系統的某一具體的運動狀態,才能討論其是否穩定的問題。非線性系統可能存在多個平衡狀態,其中某些平衡狀態是穩定的,而另一些是不穩定的。初始條件不同,系統的運動可能趨於不同的平衡狀態,運動的穩定性就不同。所以說非線性系統的穩定性不僅與系統的結構和參數有關,還與運動的初始條件、輸入信號有直接關係。
(2)時間回響
線性系統的時間回響與輸入信號的大小及初始條件無關。對於線性系統,輸入信號的大小只能影響回響曲線的幅值,不會改變回響曲線的形狀。而對於非線性系統而言,它的時間回響與輸入信號的大小與初始條件有關。
(3)自激振盪
線性定常系統只有在臨界穩定的情況下,才能產生周期運動,而非線性系統在沒有外界周期變化信號的作用下,系統就能產生具有固定振幅和頻率的穩定周期運動,我們稱之為自激振盪,簡稱自振,其振幅和頻率是由系統本身的特性所決定。
(4)對正弦輸入信號的回響
線性系統當輸入某一恆定幅值和不同頻率的正弦信號時,穩態輸出的幅值是頻率的單值連續函式。而非線性系統輸出的幅值與頻率的關係可能會發生跳躍諧振和多值回響。
(5)非線性系統的畸變現象
線性系統在正弦信號作用下的穩態輸出是與輸入同頻率的正弦信號;非線性系統在正弦信號作用下的穩態輸出不是正弦信號,而是包含有倍頻和分頻等各種諧波分量,使波形發生非線性畸變。
相對於線性控制,非線性控制具有以下優點:
1)改善控制性能
當系統運行於小範圍內,基於線性模型假設的線性控制方法是有效的。但當系統運行於大範圍時,系統的非線性特性無法利用線性控制器進行補償,控制性能必然低下甚至系統不穩定。而非線性控制器可以直接對系統大範圍運行的非線性問題進行處理。
2)分析強非線性
所謂的強非線性包括飽和、死區、嗟合間隙和磁滯等,在控制工程中經常碰到。這些非線性的作用不能由線性方法控制,而必須發展非線性分析技術。
3)處理模型不確定性
在設計線性控制器時,通常需要假設系統模型參數是已知的。但是,許多控制問題含有非線性的模型參數。這可能是由於參數隨時間緩慢變化,如水下機器人航行時水的壓力,或者是由於參數的突然變化而產生的基於不精確或失效的模型參數值的線性控制器表現出明顯的特性惡化,甚至產生不穩定現象。對此種情況,為了應對這種系統模型的不確定性,可在系統控制器中有意引入非線性。魯棒控制器和自適應控制器便是這樣的非線性控制器。
4)簡化控制系統設計
由於設計非線性控制器時經常基於被控對象的物理特性,好的非線性控制設計在有些情況下可能要比線性控制設計更簡單更直觀。例如,在某個垂直平面內的單擺,該單擺從某個任意初始角度開始擺動,並逐漸衰弱,最後停在垂線的位置。雖然單擺的特性可能在接近平衡點時可通過對系統的線性化進行分析,但是其穩定性實際上與某些線性化系統矩陣的特徵值關係很小。此例是基於下述事實:該系統的全部機械能逐漸被各種摩擦力所消耗,因此,單擺在某個最小能量位置趨於停止。
最優控制
與線性定常系統的最優控制的綜合理論和方法已非常成熟形成鮮明對比的是,對非線性系統而言,雖然人們也對其進行了廣泛的研究,然而用經典最優控制理論解決系統的綜合問題獲得的結果具有很大的局限性,對這一問題的解決仍然是相當困難的。非線性系統的非線性主要來源於系統本身的不完善性和系統的固有特性。這二者在實際系統中都是不可避免的。因此對非線性系統的次優控制這一課題的研究不但具有重要的理論價值,而且具有重要的實用價值。
這十年來,眾多學者對這一課題進行了研究。然而,在眾多的研究成果中多數是研究一些特殊情況下的特定結果,或是給出了一些描述性的結果。其中Hager給出了基於乘法器的非線性系統最優控制方法。Teo等研究了具有不等式約束的非線性系統最優控制問題。Alt討論了帶約束的非線性最優控制系統的穩定性問題。Sokhin研究了用波動方程描述的非線性系統的最優控制問題。De Figueired等研究在擾動作用下非線性系統的最優控制。BeCerra等研究了非線性離散系統的最優控制問題,給出了最優參數的估計式。SotjnaoviC研究了橢圓型非線性系統的最優衰減控制問題。以上所提出的最優控制方法和方案,基本上限於理論研究方面。對具體的非線性系統,實現最優控制是非常困難的。近年來,人們提出了若干新方法。如Hirasawa等套用人工神經網路的學習功能,提出了PLN模型,並研究了其在非線性系統的控制問題中的套用。但由於人工神經網路線上學習的實時性難以保證良好的控制指標。為了便於工程實施,人們常不一味追求系統的最優性能指標。因此,提出了若干次優控制方法。Ngaurka等給出了基於Fourier級數的非線性系統的最優控制方案。這一方法對求系統的次優控制比較方便。Newman等研究了二階非線性系統的次優控制並進行了魯棒性分析。席裕庚等用預測控制方法研究了非線性系統的次優性,通過分析預測控制的有限時域滾動最佳化性質,得到了預測控制次優性的上界。
離散系統
早在五十年代,由於數字計算機在工程和科學上套用的增加,離散控制系統的研究己經引起了人們的注意,當時的工作主要是套用z變換研究採樣數據系統。近三十年來,離散控制系統的研究已經有了較大的發展。尤其是近幾十年來,隨著科學技術的高速發展,人類社會進入到信息化,工業技術發生了根本性變革,出現了一大批高新技術領域世界範圍的微電子技術革命浪潮,極大地推動了微處理機和微型計算機在控制系統種的套用。由於數字計算機進行計算機時在時間上是離散的,因此當一個系統用數字計算機進行控制或用數字計算機模擬、分析、設計控制系統時,需要把時間變數考慮為離散變數,研究的系統需要考慮為離散系統,由於這些原因,近來離散控制系統的研究再次引起了控制界的特別重視,目前離散控制系統的分析與設計已成為控制理論的一個重要組成部分。
隨著微型機的多功能性及可靠性的不斷提高,加之其價格的日益下降,套用微型計算機進行控制和管理日益廣泛。例如用小型機代替二次儀表對生產過程進行控制時,其不僅可以實現PID控制,還可以實現一些複雜控制。更進一步,還可以套用離散控制系統的理論和方法,設計更高級的反饋系統,以達到諸如最優控制、線性多變數控制、自適應控制等等。又如用微機對一個工廠、一個公司以至一個比較複雜的管理系統管理時,通過建立數學模型,利用離散系統的理論和方法進行分析與設計,可以得到令人滿意的管理策略。由於數字計算機處理的只能時離散的數位訊號,所以,不論它用於控制或用於管理,如果原來的信號時連續的,都需要將它離散化,轉換成離散信號。這就是說,需要通過離散化把原來的連續控制系統轉換成一個離散控制系統來處理。因此研究離散系統具有重要的現實意義。
控制方法
鑒於很多科學和工程領域對於非線性控制方法的研究和套用湧現出了極大的需求,以及計算機的廣泛使用使得離散非線性系統的控制方法研究成為必然。離散系統的研究方法一般通過Z變換建立其數學模型,然後對此模型進行研究和設計,或者對連續系統數學模型進行離散化,並將對連續系統的分析與設計方法推廣到相應的離散系統上來常見的離散控制方法有離散滑模控制方法、離散神經網路自適應控制方法、離散反步法、預測控制等。例如,針對一類三角結構的多輸入-多輸出離散非線性系統進行研究,提出了基於反步法的自適應神經網路控制算法;套用多層神經網路研究離散非線性系統的保性能控制問題;並在其基礎上進一步討論了帶有輸入約束的離散非線性系統控制問題;基於反步法和神經網路自適應控制方法分別設計了一種適用於嚴格反饋形式的離散非線性系統和飛行器的控制器;套用神經網路預測控制方法研究了一類純反饋離散非線性系統的控制問題;針對多輸入多輸出的離散非線性系統設計了一種神經網路自適應控制器;針對不確定離散系統,提出一種新型的離散趨近律,構造理想切換動態,改善了控制品質。把離散非仿射系統分解成一個線性部分和一個非線性部分,非線性部分用神經網路自適應進行控制;討論了神經網路自適應問題但是要求未知離散系統在操作點必須是可量測的。預測控制方法是一種基於離散模型提出的控制算法,預測控制的提出和套用使得離散非系統的研究再次引起了控制理論界的特別重視。由於離散非線性系統本身的複雜性,這方面還有一系列的問題有待研究,仍有大量的研究工作要做。