自適應逆控制
自適應逆控制(AdaptivelnverseControl)是由美國史丹福大學著名教授B．Widrow於1986年首次命名並提出來的，當時在學術界引起了很大反響，為設計控制系統和調節器開闢了新途徑。它是用自適應濾波方法辨識出被控對象的逆模型，串聯到對象的輸入端作為控制器來控制對象的動態特性，所以稱為自適應逆控制。自適應逆控制中的反饋是屬於局部反饋，在自適應疊代過程中只用於改變模型參數，並不直接控制主迴路中的信號流動，更沒有輸出到輸入的閉環，所以它是開環控制。自適應逆控制系統中的動態特性控制和消除擾動控制是分開來各自獨立完成的，互不影響，所以可盡最大可能提高各自的性能。所以自適應逆控制與傳統反饋控制和自適應控制在原理上截然不同。
從自適應逆控制的基本理論和方法來看：自適應逆控制涉及到自適應數位訊號處理和控制兩個學科(交叉)，也就是用自適應數位訊號處理的方法來研究未知系統自適應逆控制問題。
從所需要的數學基礎來看：自適應逆控制主要涉及機率、數理統計和矩陣代數等知識：而自適應控制還需要除此之外的一些高深數學，使廣大控制工程師們難以掌握，更難以套用。
從適用範圍來看：對象是穩定的和不穩定的；最小相位的和非最小相位的：線性的和非線性的，單輸人單輸出和多輸人多輸出等系統的控制問題。並能解決自適應控制所不能解決的問題。
非線性自適應逆控制的成立
自適應逆控制和自適應濾波的簡單比較：
在已經過去的20年中，各種期刊和會議論文集已發表了大量自適應控制方面的論文，與此同時，也刊出了很多自適應信號處理方面的論文，並出版了不少專著。這兩種學派幾乎是各自獨立發展著。大體上來說：控制理論工作者在研究自適應控制時，是用狀態變數進行反饋，通過設計出來的自適應律來調節參數(或稱為權係數)，達到控制對象的性能和抑制擾動的目的。非線性自適應逆控制及其套用(或稱為權係數)進行適時調整(或稱為自適應調整)，用這樣的方法得到的線性或非線性自適應濾波器用到線性或非線性信號處理系統中去，它們各自找到了套用的場合。
自適應逆控制已作為一種新的控制方法套用於複雜、未知和不確定的非線性動態系統控制中。它用被控對象逆的傳遞函式作為控制器，這個控制器能夠自適應的調節自身參數使得對象的動態回響達到最優。當然，要實現這一目的主要依靠逆模型，可是在實際套用中，對於一個複雜的、未知的和不確定的非線性對象模型，怎樣設計其精確的逆模型，仍是逆控制套用於實際的障礙。
自適應逆控制原理在很多文獻中已經得到套用，但是對於非線性對象的控制仍不夠完善。本書將自適應逆控制套用於非線性單輸入單輸出(SISO，Singlel：真putSingleOutput)對象控制，此外，有些方法也可推廣到非線性多輸人多輸出(MIMO，MultiplylnputMultiplyOutput)對象中去用更複雜的系統來控制。嚴格的來說，自適應逆控制方法能否套用，取決於非線性系統的逆的存在性和準確性，這將在後面說明。在這種情況下，非線性對象的逆控制能夠做到，而且通過採用非線性濾波也能做到對非線性對象的擾動進行控制。
綜上所述，非線性自適應逆控制的成立主要基於兩個方面:
(1)非線性模型和算法能夠對任意的非線性模型有逼近能力，即能夠對任意的非線性系統進行精確的建模。
(2)非線性系統的逆模型的存在性和精確性。
基本原理
不同於前面給出的傳統反恢控制和自適應控制方式，從某種意義上說是一個開環控制，而前者是閉環控制。它是藉助於自適應德波方面的知識建立起來的控制方式—自適應逆控制，這種控制方式便於理解和套用。
如圖所示為自適應逆控制的方框圖：用非線性對象傳遞函式的逆作為控制器去馭動對象，因為對象是未知的，這就要先辨識出對象的逆，並用某一種自適應算法調節控制器參數使得對象輸出與指令輸人誤差方差最小。這樣非線性對象輸出就跟隨上指令輸人。從圖可看出，只有控制器是對象傳遞函式的逆時，上臂傳遞函式才是1，與指令輸人之差最小，在理想情況下是0。
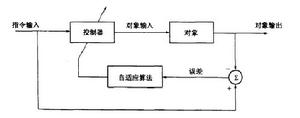非線性自適應逆控制上述結果是假定對象為非線性的、參數是慢時變的(在調整過程中認為參數不變可按定常處理)，這可看成是準靜態平穩時才成立，與MRACS的假定是相同的。
模型參考自適應逆控制
有時要求對象跟蹤的不是指令愉人而是參考模型愉出，如圖所示，這時稱為模型參考自適應逆控制系統。參考模型的動態回響應選擇與對象期望的動態回響一致。當誤差趨向於0時，對象便跟隨上參考模型，模型的性能指標便是對象的性能指標。這裡用的性能指標是模型和對象動態回響誤差方差最小。這時上臂控制器與對象串聯的傳遞函式近似等於參考模型的傳遞函式，在理想情況下二者相等。
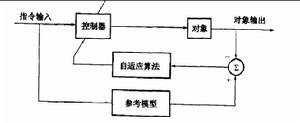非線性自適應逆控制適應逆控制中消除對象擾動和感測器噪聲環節
如圖所示，對象輸出存在著擾動和測量噪聲。為使對象輸出或動態回響中不存在噪聲和擾動，提高對象輸出的動態品質，就要想辦法將其去掉。怎樣去掉呢?圖中給出了消除辦法：將辨識出的對象模型與對象並聯，在同一個對象輸人作用下比較其輸出，則兩者的偏差就近似等於對象擾動和測量噪聲之和，在辨識模型是理想的情況下，二者之差便完全等於對象擾動和測量噪聲之和。
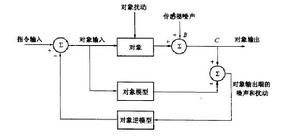非線性自適應逆控制非線性自適應逆控制可行性
要想實現非線性自適應逆控制，起決定性作用的是非線性系統建模的精確性和穩定性。隨著神經網路、模糊控制和神經網路模糊控制等非線性算法的日趨完善。
我們能夠構造良好的非線性自適應逆控制系統。實際上，神經網路、連續函式、神經網路、模糊控制器和離散模糊專家系統之間存在數值等效關係，它們都可以逼近連續函式，且它們之間又都可以相互通近，可以構造既在計算上完全等效於模徹系統又具有神經網路結構和學習機制的混合神經網路。
非線性逆系統的求解方法
簡介
逆系統控制的基本思想是求解對象逆系統方程，然後用它進行補償，使複合系統在大範圍內成為線性或接近線性的系統。從而可採用線性系統的控制器綜合方法，設計出實用的大範圍穩定的控制器。一些學者在時域內討論了逆系統的控制器綜合方法。但所提出的方法都要求系統有比較精確的模型描述。廣義頻域回響的基礎上，構造一個非線性補償器，使補償器與對象構成的複合系統高於一階的GFRF為0。但實際上由於大部分非線性系統具有無限階Volerra核，不可能完全補償，而只能使前若干階Volerra核補償為0，使複合系統近似於線性系統。對於複合系統的控制。可以用常規的自適應控制方法進行。
頻域逆系統方法
這種綜合方法的一般步驟:
(1)計算補償器G的GFRF模型;
(2)獲得G的GFRF模型的微分方程實現;
(3)對補償後的近似線性系統，利用各種傳統控制方法設計線性控制器。
