概念
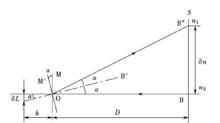非線性彈性模量對於非線性彈性模量基礎上雙模量矩形板來說，隨著非線性剛度係數的增大雙模量矩形板中心的撓度也逐漸變小，而且相同條件下非線性彈性基礎上雙模量矩形板中心的撓度要小於線性彈性基礎上雙模量矩形板中心的撓度。非線性基礎上拉壓彈性模量不同矩形板中心撓度的計算不宜採用相同彈性模量經典薄板理論，而應該採用雙模量薄板彈性理論。由於非線性基礎上拉壓彈性模量不同矩形板的彎曲變形微分方程是非線性的，因此難以求得其精確解析解，所以採用Kantorovich和Galerkin聯合法研究非線性基礎上拉壓彈性模量不同矩形板彎曲撓度，不但計算簡便而且計算精度也較高。
土體非線性彈性模量簡易計算方法
研究背景
土是地殼表層的整體岩石經過物理與化學風化作用後的產物，是由固相、液相和氣相組成的三相分散體系。長久以來，國內外已經建立的地基土的模型已不下數百個，但真正能反映土體真實面目的寥寥無幾。由於土體本身太複雜，全面地考慮土體的本構關係，則其模型參數將會因為太多而缺乏實用性。因此，從實用角度出發，建立簡易的(包括形式和參數的可得到性)、能夠反映研究問題主要矛盾的典型模型是十分必要的。
土體的變形模量
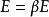非線性彈性模量根據彈性模量和變形模量的關係，可得土體的變形模量如下： 。
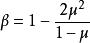非線性彈性模量其中 ，μ為土體的泊松比，它隨土的種類及結構性強弱而取不同的值，一般地說，砂性土μ=0.2-0.25，粘性土μ=0.25-0.42，理想剛體由於無側向變形μ=0，飽和土μ=0.5。關於彈性模量和變形模量的比值，理論上說，當μ從0(理想剛體)變化到0.5(理想的塑性體)時，β從1變化到0，但是實測資料表明，理論比值與實測比值存在較大的差異，而這種差異又隨土的種類與結構強弱而變化，結構性強的老年土同拘差異較大，反之結構性弱的新近沉積的粘土則較接近理論值。
研究結論
研究根據彈性模量和變形模量曲線的關係，建立了一個土體非線性彈性模量簡易計算方法，並將其套用於某實際工程，計算結果表明本文的方法更符合實際。儘管利用本文的簡易計算方法進行沉降計算的結果比較接近於實測沉降預估值，相對於傳統的計算有極大的改進，但是二者仍然有一定的差距。分析產生偏差的產生可知，這主要是由於土體受到了較大的擾動，地質報告提供的參數偏小，計算沉降量偏大等原因造成的。因此，土樣採集時儘可能少的擾動土體，保持土體本身物理力學性質的穩定性，使沉降計算時取用的土體物理力學指標能夠真實的反映土體的本來性質，這是達到理論計算值和實測沉降預估值相接近的一個十分重要的前提條件。
非線性彈性模量對波速影響的實驗研究
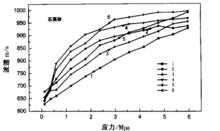圖1 石英砂在循環應力下的波速變化地球表層的岩石和土壤含有大量的孔隙和裂縫，可以認為是一種鬆散介質，具有非線性彈性的特徵。在循環應力的作用下，介質的非線性彈性使應力一應變曲線變成滯迴圈。對此問題，MaCall利用P—M模型，對滯回曲線的產生和對波速的影響進行了研究。同時也對非線性彈性對波的頻散，波形的畸變等問題進行了理論推導。而Meagan對非線性彈性波傳播進行了實驗研究。在他們的研究中，應力或深度或速度作為參量是相對固定的。在波的傳播過程中，由於波的振幅變化，使應力、應變和模量也產生了微小的非線性變化，從而導致了波的頻散、畸變和衰減等一系列複雜現象。
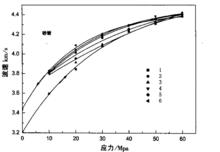圖2 砂岩在循環應力下的波速變化實驗研究主要是考慮壓力或深度作為自變數且大幅度變化時對波速所產生的影響，特別是在循環應力的條件下波速的變化規律。波速是介質的重要參數，它也受到非線性彈性的明顯影響，使得波速-應力曲線與應力-應變曲線相似，也變成了滯迴圈。波速成為壓力的多值函式，給實際問題的處理帶來了不確定性。因此我們希望能將速度對應力的多值函式轉化為速度對某參量的單值函式。
用實驗的方法，通過測量得到應力、應變、波速等有關參數，對非線形模量與應變的關係作了非線性擬合；用非線性模量來代替彈性模量，對彈性介質中的波速公式作了修正。將波速轉化成應變(或密度)的單值函式。
實驗結果
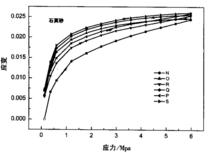圖3 石英砂的應力一應變曲線圖1和圖2顯示，速度是應力的多值函式。速度不僅與應力大小有關，還與應力變化的方向和循環次數有關。相應於應力的每一個循環，波速也產生一個循環。在每一個循環中，卸載時的波速高於載入時的波速。而後一次循環的波速要高於前一次循環的波速，表示介質在不斷被壓實，而且產生了應變相對於應力的延遲或滯後。
石英砂的應力一應變曲線如圖3所示。應力應變的關係是非線性的。每次應力循環時都產生了殘餘應變。其大致形狀與速度一應力曲線相似。由於速度是應力的多值函式，給實際問題的處理帶來了不確定性，因此我們希望能將速度對應力的多值函式轉化為速度對應變的單值函式。
石英砂對非線性模量和波速的影響
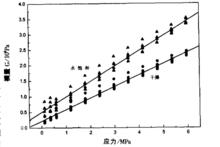圖4 石英砂在循環應力下的模量變化先通過活塞上的小孔使石英砂處≥於水飽和狀態，然後再進行循環加卸載實驗。因為孔隙中充滿了水，使得介質較難壓縮。圖4是石英砂處於乾燥和水飽和兩種狀態下的模量與應力的關係。模量隨應力的變化與隨應變的變化不同，近似於直線，但都隨應力增加而增加。水飽和時的模量與乾燥狀態相比有明顯的提高，而且隨應力的增加速率更快。同時，在水飽和的條件下，波速也有明顯的提高。由於不斷緩慢排水的緣故，波速測量精度較低，數據比較分散，但大體上還是與計算擬合曲線相近。
討論與結論
地球表面的介質，如岩石和土壤。在實際工作中，可採用四種不同的模型來進行研究，即線性彈性體、非線性彈性體、塑性體和粘彈體。後三種模型，在循環應力作用下，都會產生應力一應變的滯迴圈。本文採用的是非線性彈性體模型。在應力由上升轉為下降時，由於應變的滯後，由應力差與應變差之比定義的模量會出現突變。這是由於裂紋的打開和關閉壓力不同所造成的。在P—M模型中有較為詳細的討論。
模量隨應力的突變給波速的計算帶來了困難，但由於模量相對於應變是連續的，是不變的，因此用應變來替代模量和應力，非彈性模量與應變的關係。水飽和將使介質變硬，與乾燥狀態相比，模量不但數值大，而且上升速率快。但波速與應變的單值函式依然存在，只是常數C和B的值有所不同。利用本文的有關公式，可通過岩石樣品的應力應變曲線來預測其波速在不同壓力狀態或不同深度時的變化。
