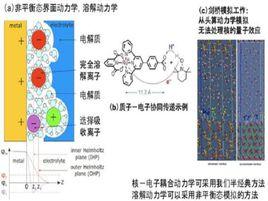
非平衡態的概述
系統中狀態變數不是常量的定常狀態。平衡態可看作是周期運動中振幅收縮到零的極限情況。與平衡態一樣,非平衡態也有穩定和不穩定兩類。狹義的非平衡態指穩定的非平衡態。在動態系統中穩定的定常狀態稱為系統的吸引子。除混沌態以外的穩定定常狀態稱為平庸吸引子,而奇異吸引子則指混沌這種非平衡態。
例如用邏輯斯蒂映射描述生態系統中某一種群數量的動態規律為:
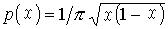 非平衡態
非平衡態=λ(1-) 0≤≤1=0,1,2,… 0≤λ≤4
式中為狀態變數,表示該種群數量與某個特徵數(最大可能的個數)之比,為離散時間(第代),λ為控制參量。當λ≤3時,系統的終態是平衡態。當 3<λ<4時,系統的終態是非平衡態。當λ=3.5時,系統的終態是每4 代重複一次的周期解:0.383、0.827、0.501、0.875、0.383、0.827、0.501、0.875…,這種循環即為非平衡態。當λ=4時,系統的終態是在0和1之間(好像)隨機地取值,沒有穩定的循環出現,但終態以確定的機率密度分布()出現於0和1之間:
非平衡態熱力學
非平衡態熱力學被用來不是熱力學平衡,但可以分成足夠小的系統在還夠大到可以就熱力學套用在它身上的子系統的研究系統上。此一假設被稱為局部平衡。在某些例子中,有一堆分離的系統經由一堆分離的接連來相互作用著。連續系統則由測量每單位體積的外延量(如密度)及認為內涵量有局部定義的值來研究;這表示所有的熱力學變數都可以用場來表示。內涵量的不同或梯度被稱為熱力學作用力,且會導致外延量的流動。
當一開放系統被允許達到一隱定態時,它會安排地讓它自己達到最小的總熵值。此一被伊利亞·普里高津和其他人所重視的原理允許我們使用變分原理來公式化隱定態非平衡態熱力學。另一個有力的工具為昂薩格倒易關係,它表示在兩個流動至其他的不同熱力學作用力的反應之間有著某些對稱。
非平衡態統計物理
非平衡態統計物理中的熵產生概念是用來描述該非平衡定態距離平衡態遠近的物理量,這和非平衡態統計物理中另一個巨觀可逆性的概念相聯繫。一個巨觀不可逆的定態系統必須具有正的熵產生,且非平衡 。
非平衡態統計力學
當濃度、溫度、或流體的運動速度在空間分布不均勻時,系統處於 非平衡態,將產生物質、熱量或動量的傳遞。其他如電磁輻射的吸收、光的彈性散射、準彈性散射和非彈性散射、中子散射、介電弛豫和分子光譜等,都涉及非平衡態。實際過程的產生均起源於非平衡態。隨時間流逝由非平衡態趨向平衡態是所有實際過程的共同特徵。在分子水平上研究非平衡態的特點,將微觀的分子性質與巨觀的非平衡態的性質聯繫起來,是非平衡態統計力學的任務 。