簡介
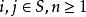 非常返狀態
非常返狀態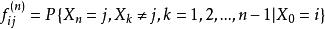 非常返狀態
非常返狀態設任意的 稱 為馬氏鏈在0時從狀態i出發,經n步轉移後,首次到達狀態j的機率。簡稱首達機率。
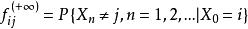 非常返狀態
非常返狀態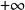 非常返狀態
非常返狀態記 ,稱為馬氏鏈在0時從狀態i出發,永遠不能轉移到 狀態j的機率。
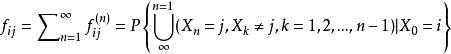 非常返狀態
非常返狀態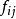 非常返狀態
非常返狀態又記 ,稱 為馬氏鏈在0時從狀態i出發,經有限步轉移後終究到達狀態j的機率(也稱遲早機率)。
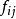 非常返狀態
非常返狀態特別的,當i=j時,表示馬氏鏈在0時從狀態i出發,經有限步轉移後終究返回狀態i的機率。
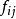 非常返狀態
非常返狀態利用機率可以定義狀態類型:
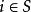 非常返狀態
非常返狀態設狀態
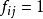 非常返狀態
非常返狀態(1)若 則稱狀態i是常返的(返回的);
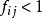 非常返狀態
非常返狀態(2)若 則稱狀態i是非常返的(滑過狀態)。
當i為常返態時,也就有
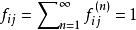 非常返狀態
非常返狀態 非常返狀態
非常返狀態即 構成機率分布,則相應的數學期望為
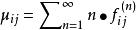 非常返狀態
非常返狀態 非常返狀態
非常返狀態則 表示馬氏鏈從狀態i出發首次再返回狀態i的平均時間(或平均轉移步數)。
 非常返狀態
非常返狀態利用量 可以進一步定義狀態類型:
 非常返狀態
非常返狀態(1)若 則稱狀態i為正常返狀態;
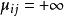 非常返狀態
非常返狀態(2)若 則稱狀態i為零常返狀態(消極常返狀態)。
狀態類型的判斷
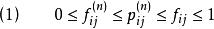 非常返狀態
非常返狀態 非常返狀態
非常返狀態 非常返狀態
非常返狀態定理
定理1
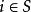 非常返狀態
非常返狀態設狀態 ,則
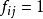 非常返狀態
非常返狀態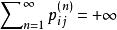 非常返狀態
非常返狀態(1)狀態i是常返的( )充要條件為
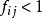 非常返狀態
非常返狀態(2)狀態i是非常返的( )充要條件為
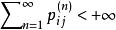 非常返狀態
非常返狀態定理2
齊次馬氏鏈的狀態空間S可唯一地分解為有限或可列無限多個互不相交的狀態子集的並。即
 非常返狀態
非常返狀態其中D是所有非常返狀態構成的狀態子集。
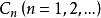 非常返狀態
非常返狀態均是由常返態構成的不可約閉集。
每個狀態子集中的狀態有著相同的狀態類型:即 或者均為零常返,或者均為正常返非周期,或者均為正常返周期且周期相同。
定理3
設X是狀態有限的齊次馬氏鏈, 則
(1) X的非常返狀態集D不可能是閉集;
(2) X不存在零常返狀態;
(3) 若X是不可約的, 則X所有的狀態都是正常返的。
舉例
設狀態空間S={1, 2, 3, 4}的馬爾可夫鏈,它的一步轉移機率矩陣為
 非常返狀態
非常返狀態試分析馬氏鏈的狀態的常返與否。
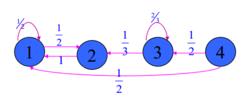
解:馬氏鏈的狀態轉移圖為
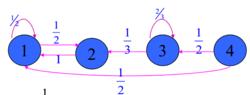 非常返狀態
非常返狀態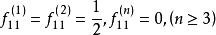 非常返狀態
非常返狀態因為
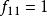 非常返狀態
非常返狀態所以 ,所以狀態常返。
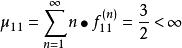 非常返狀態
非常返狀態又 ,故狀態1正常返。
 非常返狀態
非常返狀態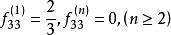 非常返狀態
非常返狀態因為
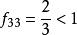 非常返狀態
非常返狀態所以 ,故狀態3非常返。
類似可以討論狀態2和4。
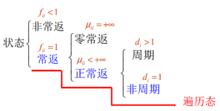
因此可用下面的圖來表示各狀態的關係:
 非常返狀態
非常返狀態