電路的穩定性
正文
動態電路在運行中受到各種擾動而不引起工作狀態的質的變化,或擾動消失後能返回(或接近於)原來的工作狀態的性質。穩定是電路能正常工作的必要條件。穩定性問題涉及電路中電流、電壓的變化,因此它只在動態電路(含電感、電容等元件的電路)里才出現。而實際電路一定存在電感(例如導線的電感)、電容(如導體間的電容),它們都是動態電路,因而總存在穩定性問題。線性定常電路的穩定性 線性定常 n階電路的電路方程是常係數n階常微分方程。例如電阻R、電感L串聯電路的電路方程是一階常微分方程:
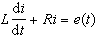
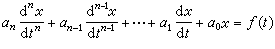
anPn+a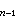 P
P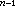 +…a1P+a0=0
+…a1P+a0=0
非線性電路的穩定性問題 許多非線性電路的電路方程可用狀態方程描述:
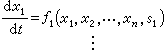
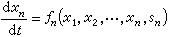
不變解的穩定性 直流電源作用於電路時,電路方程可有不變解,它代表電路中各處的電壓、電流是不隨時間變化的常量。這時所有狀態變數也是常量,記作χ10,χ20,…,χ
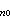 ,由狀態空間中一個不動的點P代表。該點稱不動點或平衡點(圖1)。
,由狀態空間中一個不動的點P代表。該點稱不動點或平衡點(圖1)。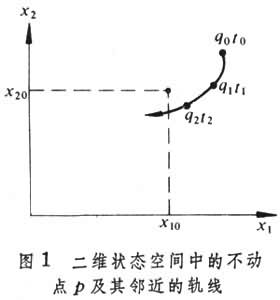 由於某種干擾,在t0時刻狀態稍許偏離了不動點P而位於P點周圍任一點q0,從t0時刻開始,由q0發出的軌線如圖1曲線所示,曲線上q1、q2分別代表t1、t2時點的位置。若對於任何時刻ti,由不動點P到qi的距離di總是很小,不動點P是穩定的,即電路不變解是穩定的。若qi最終趨於P點,不動點P是漸近穩定的,這代表雖然干擾使狀態偏離不變解,但最後狀態會回到該不變解。若qi最終遠離P點,不動點是不穩定的。
由於某種干擾,在t0時刻狀態稍許偏離了不動點P而位於P點周圍任一點q0,從t0時刻開始,由q0發出的軌線如圖1曲線所示,曲線上q1、q2分別代表t1、t2時點的位置。若對於任何時刻ti,由不動點P到qi的距離di總是很小,不動點P是穩定的,即電路不變解是穩定的。若qi最終趨於P點,不動點P是漸近穩定的,這代表雖然干擾使狀態偏離不變解,但最後狀態會回到該不變解。若qi最終遠離P點,不動點是不穩定的。 直流電源作用下,非線性電路的不變解可以不止一個,與之對應的狀態方程的不動點可以不止一個。只有那些漸近穩定的不動點才和電路的穩態解對應。
電路周期解的穩定性 電路的周期解用狀態變數表示時是χ1=φ1(t),χ2=φ2(t),…,χn=φn(t),所有φi(t)函式是t的周期函式,周期為T。在狀態空間裡,點的軌線是一條閉曲線。圖2所示為二階電路狀態空間中的閉軌線r。
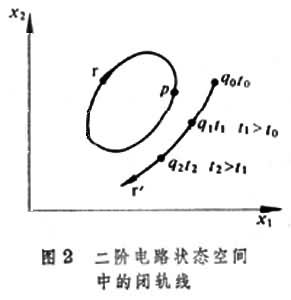 設t0時,點P的坐標是χ1=φ1(t0)、χ2=φ2(t0)。經過一個周期,即在t0+T時刻,狀態點仍位於P點。設由於某種干擾,t0時刻的狀態稍許離開 P點而是位於 P點周圍的任一點q0。從t0開始,從q0發出的軌線如圖2中曲線r┡所示,圖中,q1、q2代表t1、t2時的點的位置。若r┡最終趨於閉軌線r,稱周期解是穩定的;若r┡遠離r,稱周期解是不穩定的。只有穩定的周期解,才是電路的穩態解。
設t0時,點P的坐標是χ1=φ1(t0)、χ2=φ2(t0)。經過一個周期,即在t0+T時刻,狀態點仍位於P點。設由於某種干擾,t0時刻的狀態稍許離開 P點而是位於 P點周圍的任一點q0。從t0開始,從q0發出的軌線如圖2中曲線r┡所示,圖中,q1、q2代表t1、t2時的點的位置。若r┡最終趨於閉軌線r,稱周期解是穩定的;若r┡遠離r,稱周期解是不穩定的。只有穩定的周期解,才是電路的穩態解。 結構穩定性 電路的回響和電路參數有關。電阻、電感、電容、正弦電源的振幅和頻率等,都是電路參數。由於各種干擾,這些參數不能維持為固定不變的值,總會有微小變化。若參數的微小變化,能引起電路回響的質的變化,則在該參數下的電路稱為結構不穩定的電路,反之稱為結構穩定的電路。例如設 RLC串聯電路中的電阻R的絕對值丨R丨極小。若R>0,電路中的電壓、電流的波形是衰減振盪波形,電路是穩定的;若R<0,波形是增幅振盪波形,電路是不穩定的。這兩種波形有質的不同。R=0稱作參數R的分岔值。在分岔值的兩側,電路回響有質的變化。R=0時的電路就是結構不穩定的。R≠0時的電路是結構穩定的。設某個帶反饋的放大電路可以將信號放大。增大放大器的放大倍數β,若它超過某個分岔值β0時,電路中激起振盪。放大倍數為臨界值時的放大電路,是結構不穩定的;而β≠β0時的電路是結構穩定電路。電路參數剛好是分岔值的機率是零,因此實際電路總是結構穩定電路。但研究結構不穩定電路,對於了解電路性質的變化是有意義的。