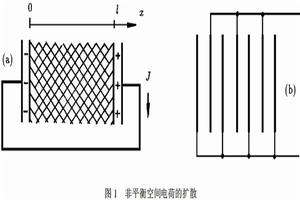
耗散反應產物的電荷擴散
電荷擴散能量相干寬度Γ分布寬度隨著同位素電荷數Z的減小有顯著的增大，反應時間越長，交換的核子數越多，其分布寬度也就越寬。圖1給出了分布寬度隨出射碎片電荷數變化的關係，r的分布寬度隨電荷數Z基本上呈線性變化。 這反映了電荷擴散過程的存在。
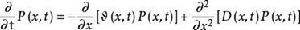電荷擴散
電荷擴散
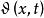電荷擴散在輸運理論框架中，一個物理量x的幾率分布函式P(x,t) 的福克一普朗克方程為： ，其中 為漂移係數， 為擴散係數。
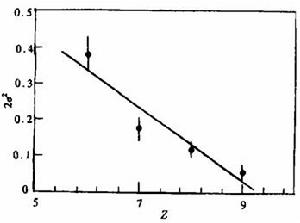
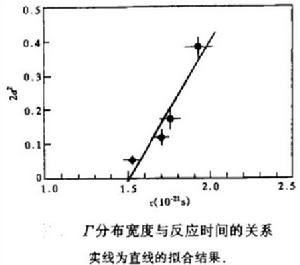
電荷擴散各元素隨原子核的中子數/電荷數Z呈高斯型的分布，誤差範圍內其平均值的變化很小，可以認為漂移速度為零。分布寬度有較大的變化，說明擴散過程是明顯存在的。圖2給出了分布寬度2σ少與平均作用時間τ的變化關係，τ根據測不準關係τ=h/Γ，分布寬度與反應時間呈線性變化的關係。直線斜率即為擴散係數2D。
空間電荷擴散理論
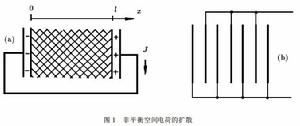
電荷擴散一般地，在高絕緣體中束縛有正和負的空間電荷，熱平衡下電中性條件要求正負電荷數目相等並有均勻分布。在圖1(a)距離為l的兩電極間充滿介質。經恆定電壓U極化達平衡後,將有N個負電荷e被排斥離開單位面積負電極。在t=0時除去U0並令兩電極短路放電,則通常熟知的各種機構提供的極化迅速消失，這些極化我們通稱為快極化，這時介質內各處電場為零。空間電荷在零場下建立新的平衡分布需較長時間,它貢獻的極化屬慢回響。
體系中的空間電荷處於束縛狀態，不是載流子；但可藉助於熱運動起伏能量的激活而位移至鄰近束縛位置以產生極化效應.在液體中，空間電荷束縛於分子中的某固定位置;它的運動反映了分子或其部分鏈段的運動。由於受到鄰近粒子的障礙，這種運動應該很慢。在熱平衡下，空間電荷的分布應使體系的巨觀極化強度為零。若有某種原因使時間t=0時空間電荷分布不均勻而產生極化強度P(t)=P0，在零場下可測出其衰減規律並記為P(t)=PF(t)；其中F(0)=1，F(∞)=0。空間電荷分布由不均勻而在零場下趨向均勻的運動可等效描述為擴散。束縛電荷的等效擴散不同於載流子的擴散。後者的擴散係數D與遷移率μ有關係eD=kTμ。等效擴散不存在類似關係，因為束縛空間電荷不能導電的假設意味著它的遷移率等於零。麥克斯韋方程表明，電位移矢量對時間的微商等效於自由電荷在外場中的遷移電流密度；在零場中束縛電荷位移的時間微商就等效於自由電荷的擴散運動。
