靜止能量
不變質量（invariant mass）或稱 內秉質量（intrinsic mass）、 固有質量（proper mass），亦常簡稱為 質量，指的是一個物體或一個物體系統由總能量和動量構成的在所有參考系下都相同的一個洛侖茲不變數。當這個系統作為整體保持靜止時，不變質量等於系統的總能量除以光速的平方，這也等於這個系統在一個與之相對靜止的秤上稱得的質量。如果系統由一個單一粒子組成，不變質量也稱作這個粒子的 靜止質量。
由於一個孤立系統的質心總保持勻速直線運動，因此觀察者總可以選擇這樣一個參考系，使系統在這一參考系中的總動量為零，即相對這個參考係為靜止。這樣的參考系稱作質心繫，這時系統的不變質量就等於系統的總能量除以光速的平方。這個於質心繫下的總能量，可以被看作是系統在不同慣性系下可能被觀測到所具有能量的“最小值”。
在多粒子系統的情形下，質心繫中的粒子彼此之間可能會存在相對運動，並有可能存在一種或多種基本相互作用。這時粒子的動能和力場的勢能會增大系統的總能量，使之大於所有粒子的靜止質量之和，這部分能量也對系統的不變質量有貢獻。
在粒子物理學中的套用
電子靜止能量
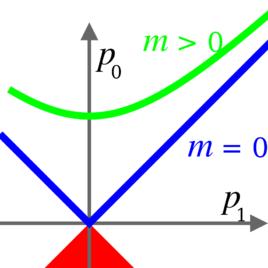
電子靜止能量在粒子物理學中，不變質量是一個粒子的能量 和動量 的數學組合，在靜止參考系中等於粒子的靜止質量。不變質量在所有參考系中的值都是相同的（參見狹義相對論）。
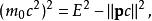電子靜止能量
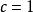電子靜止能量
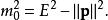電子靜止能量或者採用自然單位，從而光速 ，
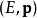電子靜止能量這個方程指出不變質量的值等於四維動量矢量 的模（長度），這裡模的計算是根據相對論性的畢達哥拉斯定理，從而空間維度和時間維度具有相反的符號。這個矢量的模在四維時空中任意的洛倫茲變換（遞升或旋轉）操作下都保持不變，正如一個普通三維矢量的長度在三維空間中進行任意旋轉變換後仍然保持不變。
由於在粒子衰變過程中，粒子系統的不變質量是由一系列能量動量等守恆量給出的，通過衰變產物的能量和動量所計算得到的不變質量等於衰變前粒子的質量。一個粒子系統的質量可由一個普遍公式給出：
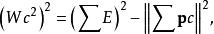電子靜止能量
電子靜止能量
電子靜止能量
電子靜止能量其中 是粒子系統的不變質量，等於衰變粒子的質量， 是粒子能量的標量和， 是粒子動量的矢量和。
套用舉例：兩粒子碰撞
在兩粒子碰撞（或兩粒子的衰變）過程中，不變質量的平方在自然單位下為
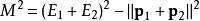電子靜止能量
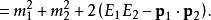電子靜止能量靜止能量
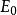電子靜止能量一個粒子的 靜止能量被定義為：
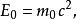電子靜止能量
電子靜止能量其中 是真空中的光速。一般而言，只有能量的差值才有物理意義。因此定義一個靜止能量能夠使能量變化的衡量有一個絕對的基準。
定義靜止能量的動機來自於狹義相對論，根據這一理論，一個物體的質量變化正比於其動能，即
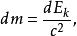電子靜止能量這個關係引出了愛因斯坦著名的結論：能量和質量是同一現象的兩種表現。定義上述的靜止質量能夠使質能等價的數學表達更為優雅，但不足之處是它將能量都用一個絕對的基準來量度的做法仍然顯得有些隨意。
參見
•狹義相對論中的質量
•不變數
