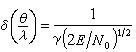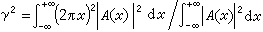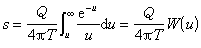雷達測量精度

雷達測量正確性或誤差大小的量度。測量誤差很小。

雷達測量精度

正文

雷達測量正確性或誤差大小的量度。測量誤差，一般用測量值與真實值之差的平方的統計期望值（均方誤差）或平方根（均方根誤差）來表示。雷達所測量的目標參數通常包括目標距離(回波時延)、距離變化率（都卜勒頻移）、方位角和俯仰角（回波到達角）等。現代雷達還能測量目標尺寸、形狀和其他參數。測量精度的根本限制因素是噪聲。根據參量估計理論可以求出雷達測量的極限精度，並把它作為設計和評價雷達的重要依據之一。
雷達回波由信號s(t-T)加噪聲n(t)組成，式中T是回波信號的時延。時延T的估計值的均方根誤差的下限為

式中

分別為信號能量和有效頻寬;N0為噪聲的功率譜密度(即單位頻寬內的噪聲功率)；s(f)為s(t)的傅立葉變換。都卜勒頻移的估計值的均方根誤差的下限為

式中

為信號的有效時寬。
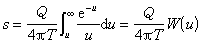
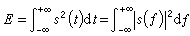
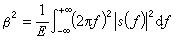
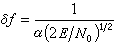
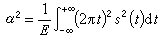
對於任意波形總有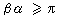。因此

這說明,只要有足夠大的信噪比E/N0並選擇βα足夠大的雷達信號，測量時延（距離）和頻移（速度）均可獲得所希望的精確程度。
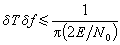
由於天線方向圖G(θ)和天線口徑面上場的幅度分布A(x)之間也近似有傅立葉變換的關係，可以同樣求得角度估值的均方根誤差的下限為

式中

γ稱為有效口徑寬度；λ為雷達波長。因此，雷達測量精度與雷達波形有密切關係。

配圖

相關連線