背景
常規的反饋控制僅利用了當前控制時刻的信息,當目標輸入變化時,會因控制滯後而產生跟蹤誤差,因而僅利用常規的反饋控制不能滿足高精度跟蹤的要求。跟蹤誤差如從頻域分析,可以分為由幅值誤差引起的和由相位誤差引起的兩部分。為了減小誤差,可考慮對它們分別進行補償。對於前者可以用.放大器進行補償,對於後者則可採取零極點對消的辦法來進行相位補償,但這種方法只適用於最小相位系統.對於非最小相位系統,接此原則設計系統剮會導致不希望的零極點對消。
為避免這一點,Tomizuka等人在1987年提出了採用預見控制,利用未來信息使從目標輸到控制輸出的相位差在全頻率域內補償到0的設計方案,即零相位跟蹤控制(ZPETC) 。1992年舟橋康行、山田學在文獻 的基礎上,採用兩自由度控制系統的設計方法來設計零相位跟蹤控制器,不僅將從目標輸入到控制輸出的相位差在壘頻率域內補償到 0,而且可謂整控制系統的增益特性 。但是他所針對的典型信號中沒有包括正弦信號,在跟蹤正弦信號時,仍存在幅值誤差,而且其設計過程比較複雜,不便於實際套用。
基本原理
零相位跟蹤控制的基本原理就是採用預見控制,利用已知的未來信息設計一補償器,使從目標輸入到控制輸出的相位在全頻率域內為0。其基本結構如圖1所示。
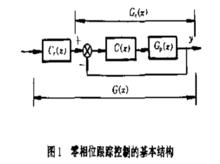 零相位跟蹤控制
零相位跟蹤控制 零相位跟蹤控制
零相位跟蹤控制 零相位跟蹤控制
零相位跟蹤控制 零相位跟蹤控制
零相位跟蹤控制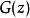 零相位跟蹤控制
零相位跟蹤控制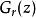 零相位跟蹤控制
零相位跟蹤控制其中, 分別表示目標輸入、控制輸出和離散時間控制對象, 是以穩定性為目的而設計的反饋控制器, 是以跟蹤性為目的而設計的零相位跟蹤控制器。假設已經設計好了,並使系統能穩定運行,那么關鍵問題是如何設計 。
設控制對象和反饋控制器組成的閉環傳遞函式為
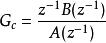 零相位跟蹤控制
零相位跟蹤控制 零相位跟蹤控制
零相位跟蹤控制上式中, 表示計算時間在內的設備的死區時間。
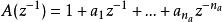 零相位跟蹤控制
零相位跟蹤控制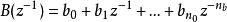 零相位跟蹤控制
零相位跟蹤控制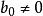 零相位跟蹤控制
零相位跟蹤控制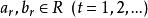 零相位跟蹤控制
零相位跟蹤控制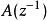 零相位跟蹤控制
零相位跟蹤控制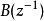 零相位跟蹤控制
零相位跟蹤控制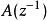 零相位跟蹤控制
零相位跟蹤控制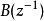 零相位跟蹤控制
零相位跟蹤控制其中, , , 和 是既約的,並且, 是一個全部根能消去的穩定的多項式。把 按如下公式分解:
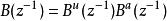 零相位跟蹤控制
零相位跟蹤控制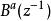 零相位跟蹤控制
零相位跟蹤控制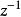 零相位跟蹤控制
零相位跟蹤控制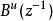 零相位跟蹤控制
零相位跟蹤控制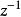 零相位跟蹤控制
零相位跟蹤控制其中, 為由單位圓內的零點組成的 的多項式, 為由單位圓外和單位圓上的零點組成的 的多項式。
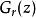 零相位跟蹤控制
零相位跟蹤控制根據Tomizuka提出的零相位跟蹤控制器設計方法,零相位跟蹤控制器 可表示為
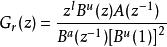 零相位跟蹤控制
零相位跟蹤控制存在的問題:
由於零相位跟蹤控制是基於零極點對消的辦法來進行相位和幅值補償的,因而對參數變化和擾動非常敏感,而且還存在著一定的建模誤差所以,按上述方法設計的零相位跟蹤控制器在實際套用中並不能很好地改善跟蹤性能。
一些改進
文獻 通過參數線上辨識,線上動態調整零相位跟蹤控制器的參數來克服參數的變化,使零相位跟蹤控制器能與變化的系統保持一致,該方法的缺點在於參數自適應算法複雜,不易保證實時性。
文獻 則從伺服系統的內環著手,通過魯棒控制器來補償機械非線性、擾動和參數的變化,使實際的閉環系統與名義系統相屙,然後按名義系統設計零相位跟蹤控制器,該方案較好地克服了零相位跟蹤控制器的缺點,但是性能優良的魯棒控制器卻不易設計。
