模型簡介
1982年，C.E.Garcia和M.Morari提出具有模型、控制、反饋環節的內模控制結構，其產生背景主要有兩個方面：一是對當時的兩種預測控制算法MAC和DMC進行系統分析；其次是作為Smith預估器的一種擴展，其設計更為簡單，魯棒性及抗干擾性大為改善。
內模控制(Internal Model Control,簡稱IMC)是一種基於過程數學模型進行控制器設計的新型控制策略。IMC具有實用性強，結構簡單，設計直觀，不需要精確的對象模型，線上調節參數少，調整容易等優點。特別是對於魯棒性及抗干擾性的改善和對大時滯系統的控制，效果尤為顯著，而且也為非線性系統的控制提供了一條有效的途徑。由於具有良好的跟蹤性能和抗干擾能力，並對模型失配有一定的魯棒性，使其在工業過程控制中獲得了越來越廣泛的套用。
此外，內模控制還和許多其它控制方式相結合，如內模控制與模糊控制、內模控制和自適應控制、內模控制和最優控制、預測控制的結合使內模控制不斷得到改進並廣泛套用於工程實踐中，取得了良好的效果。
基本原理
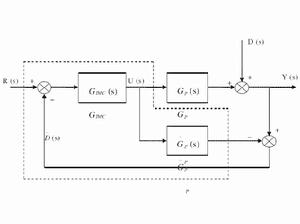
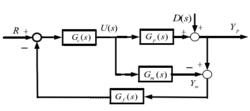圖1 IMC的基本結構如圖1所示的是內模控制的一般結構圖，其中，U ( s )為輸入變數，R為設定值，D ( s )為外部干擾項Yp、Ym分別為對象輸出和內部模型輸出；Gp(s)為被控對象；Gm(s)為內部模型；Gc(s)為內模控制器；Gf(s)為反饋濾波器。
根據圖1，可以表示出內模控制器的閉環輸出為(式1)：
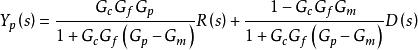內模控制
內模控制當Gf=1時，該系統為1自由度系統，可以通過調節控制器Gc來改善系統的動態伺服特性、抗干擾性和魯棒性能；當Gf 1時，該系統變為2自由度系統，反饋濾波器Gf的存在可以幫助調節系統動態回響特性和穩態特性間的平衡，綜合提高被控系統的控制品質。
基本性質
當系統為1自由度系統，即Gf=1時，內模控制器有以下三個基本性質：對偶穩定性、理想控制器特性和零穩態偏差特性。
內模控制的對偶穩定性
在 Gp(s)= Gm(s)，即模型精確匹配時，圖1所示的可等效為開環結構，意味著只要滿足穩定條件，即控制器以及對象都是穩定的，那么有系統是閉環穩定的，這就客觀上保證了內模控制系統的穩定性。對偶穩定性的重大意義在於簡化了系統穩定性的分析，特別是對於複雜的大滯後對象、非線性對象的研究，可以極大程度減少運算，提高控制系統設計的整體效率。
內模控制的理想控制特性
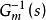內模控制不妨設 Gp(s)= Gm(s)，且Gp(s)穩定，若存在內模控制器Gc(s)= ，且對象模型的逆物理可實現時，無論外界干擾D ( s )是否為0，都有輸出Y ( s ) =R ( s)，說明 IMC 可消除干擾，實現理想控制。
內模控制的零穩態偏差特性
由(式1)可表示IMC系統的閉環偏差為：
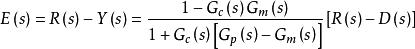內模控制
內模控制
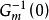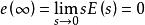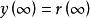內模控制
內模控制對於上式，假設滿足條件，控制器的穩態增益和模型的逆是相等的，即Gc(0)= ，則可求得E ( s )=0；再由終值定理，有 ，則 。無論對象與模型是否匹配，都能保證輸出值最終穩定達到設定值，實現了系統對於常值干擾和階躍干擾的無穩態偏差控制。這一零穩態偏差特性說明 IMC 結構本身具有積分作用，無需在控制器設計過程中引入積分項。
控制存在問題
由於實際生產條件與理論研究有較大偏差，理想的內模控制是無法實現的。比如：
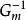內模控制(1)模型存在非最小相位部分會導致 存在超前項，物理上無法實現該控制器；
(2)當模型Gm(s)嚴格正則時，其逆也就是理想控制器就非正則，此時控制器的微分環節會使得對於干擾異常敏感；
(3) 當模型不確定性而產生模型失配時，IMC 的控制性能都會受到極大的影響。
設計方法
內模控制的兩步設計法能夠解決完美內模控制不可實現的問題。兩部設計法的基本思想是：首先，按照理想控制原則，設計出穩定的內模控制器(同時即可實現系統的閉環穩定)；然後，在控制器中加入濾波器結構；最後根據對象特性和期望的控制效果綜合設定控制器的結構和相關參數。具體如下：
第一步：理想控制原則設計控制器：
先對分解過程模型Gm進行如下分解：
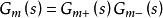內模控制
內模控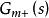制
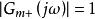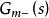內模控制
內模控制其中， 是模型的(Non-minimum Phase, NMP)部分，且滿足 ； 是對象模型中最小相位部分，穩定且不包含任何預測項。
第二步：加入濾波器結構：
為了達到期望的魯棒性和穩定性，在設計出的理想控制器中要加入濾波器結構，則內模控制器最終表達為：
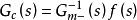內模控制其中，f ( s )是引入的n階濾波器，表示為：
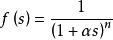內模控制
內模控制n值的選取是要保證內模控制器Gc(s)有理； 為濾波器參數，也是IMC 結構中唯一的可用於線上調節的參數，其值大小選取是否得當會直接影響閉環系統的控制特性的優劣。
