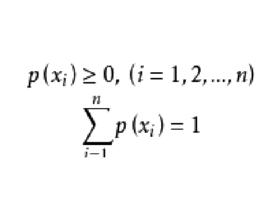離散無記憶信源的數學模型
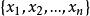 離散無記憶信源
離散無記憶信源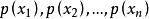 離散無記憶信源
離散無記憶信源定義 若信源X發出n個不同的符號 ,分別代表n種不同的訊息,發出各個符號的機率分別是 這些符號間彼此互不相關,且滿足
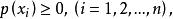 離散無記憶信源
離散無記憶信源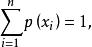 離散無記憶信源
離散無記憶信源稱這種信源為 離散無記憶信源。
離散無記憶信源是最簡單也是最基本的一類信源,可以用完備的離散型機率空間來描述,其數學模型可表示為
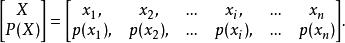 離散無記憶信源
離散無記憶信源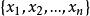 離散無記憶信源
離散無記憶信源其中n可以是有限正整數,也可以是可數無限大整數。信源輸出的訊息只可能是符號集 中的任何一個,而且每次必定選取其中一個。可見,若信源給定,其相應的機率空間就已給定;反之,若機率空間給定,也就表示相應的信源給定。所以,機率空間能夠表征離散信源的統計特性。
【 例1】在一個箱子中,有紅、黃、藍、白四種不同顏色的彩球,大小和重量完全一樣,其中紅球16個,黃球8個,藍球和白球各4個,若把從箱子中任意摸出一個球的顏色的種類作為信源,試建立其數學模型。
 離散無記憶信源
離散無記憶信源 離散無記憶信源
離散無記憶信源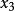 離散無記憶信源
離散無記憶信源 離散無記憶信源
離散無記憶信源解:表示摸出紅球, 表示摸出黃球, 表示摸出藍球, 表示摸出白球,則
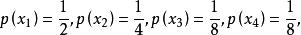 離散無記憶信源
離散無記憶信源信源的數學模型為
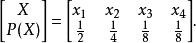 離散無記憶信源
離散無記憶信源在討論了信源的數學模型,即信源輸出的數學描述問題後,很自然地接著會提出這樣一個問題:信源發出某一符號(或某一訊息)後,它輸出多少信息量?整個信源能輸出多少信息?這就是信息的度量問題。
離散無記憶信源的信息度量
我們知道可以用機率大小來描述含有不確定性的事件。事件發生的機率越小,此事件含有的信息量就越大,獲得了信息也就消除了不確定度。隨機事件的不確定度,在數量上等於它的自信息量。因此,當信源發出的訊息不確定性越大,此訊息含有的信息量就越大。一旦訊息發出,並為接收者收到後.消除的不確定性也越大,獲得的信息也越多。離散信源可以用離散隨機變數來描述,所以我們可以用信源輸出訊息符號的不確定性作為信源輸出信息的度量。
信息量
 離散無記憶信源
離散無記憶信源 離散無記憶信源
離散無記憶信源信源X發出某一訊息符號 能提供的信息量,即 的 自信 息量(簡稱 自信息)為
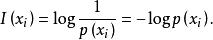 離散無記憶信源
離散無記憶信源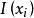 離散無記憶信源
離散無記憶信源 離散無記憶信源
離散無記憶信源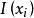 離散無記憶信源
離散無記憶信源自信息量 是指某一信源發出某一訊息符號 後所提供的信息量。自信息量 的大小隨著信源發出符號的不同而變化,不是一個確定的值,是一個隨機變數,因此不能用它作為整個信源的信息測度。而在實際中,常常需要對某個信源進行整體分析,這就要求用一個確定的值來描述信源的總體統計特徵,因此定義自信息的數學期望為信源的平均信息量,或者稱為信源的信息熵。
信源熵
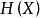 離散無記憶信源
離散無記憶信源信源各個符號的自信息的數學期望定義為信源的 平均信息量,即 信源熵,記為
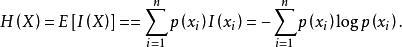 離散無記憶信源
離散無記憶信源信源熵是從平均意義上來表徵信源的總體特性的一個量,它描述了信源的統計平均不確定性。信源熵有以下幾種物理含義。
(1)在信源輸出前,信源熵表示信源的平均不確定性。
(2)在信源輸出後,信源熵表示一個信源符號所提供的平均信息量。
(3)表示信源隨機性大小,信息熵越大,隨機性越大。
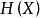 離散無記憶信源
離散無記憶信源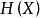 離散無記憶信源
離散無記憶信源應該注意的是:信源熵是信源的平均不確定度的描述。一般情況下它並不等於平均獲得的信息量。只有在無噪情況下,接收者才能正確無誤地接收到信源所發出的訊息,消除 大小的平均不確定性,所以獲得的平均信息量就等於 。在一般情況下獲得的信息量是兩熵之差,並不是信源熵本身。
例題解析
【 例2】投擲一枚質量均勻的硬幣,觀察正反面出現的情況,求信源熵。
 離散無記憶信源
離散無記憶信源 離散無記憶信源
離散無記憶信源解:用表示“出現正面”,表示“出現反面”,機率空間為
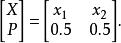 離散無記憶信源
離散無記憶信源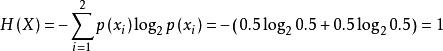 離散無記憶信源
離散無記憶信源(bit/符號)
【 例3】 計算等機率英文信源的信息熵。
解: 設26個字母和空格共27個符號等機率出現,每個符號的機率為1/27。信源熵為
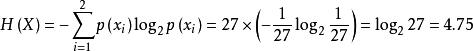 離散無記憶信源
離散無記憶信源(bit/符號)
或者可以直接套用最大離散熵定理,等機率分布信源的熵為
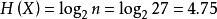 離散無記憶信源
離散無記憶信源(bit/符號)
【 例 4】 在一個箱子中,有紅、黃、藍、白四種不同顏色的彩球,大小和質量完全一樣,其中紅球16個,黃球8個,藍球和白球各4個,若把從箱子中任意摸出一個球的顏色的種類作為信源,求這個信源的熵。
解: 由題意知此信源的數學模型為
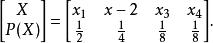 離散無記憶信源
離散無記憶信源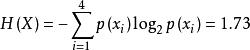 離散無記憶信源
離散無記憶信源(bit/符號)
【 例5] 現在討論一種極端的情況,二進制信源只傳送一種訊息,即永遠只傳送1或者只傳送0,求這個信源的熵。
解: 此信源發0的機率為1則發1的機率為0,或者發1的機率為1則發0的機率為0,由熵的定義式出發求得H(X)=0。
這是一個確定信源,要么發0要么發1,發出的符號是確定的,不存在不確定性。也就是說,這樣的信源,我們不能從中獲取任何信息,信源的不確定性為0。
由以上4道例題我們可以總結出以下結論。
(1)信源的熵值大小與其機率空間的訊息數和訊息的機率分布有關係。
(2)信源的訊息為等機率分布時,不確定度最大,熵值最大。
(3)信源的訊息為等機率分布,且其訊息數目越多,其不確定度越大,熵值越大。
(4)只傳送一個訊息的信源,其不確定度為0,不能提供任何信息,熵值也就為0。