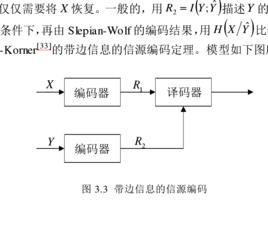
簡介
信源編碼是從信息源的符號（序列）到碼符號集（通常是bit）的映射，使得信源符號可以從二進制位元（無損信源編碼）或有一些失真（有損信源編碼）中準確恢復。在資訊理論中，信源編碼定理非正式地陳述為：
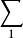信源編碼定理
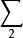信源編碼定理
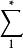信源編碼定理
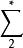信源編碼定理 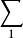信源編碼定理 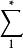信源編碼定理 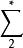信源編碼定理
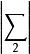信源編碼定理N 個熵均為 H(X) 的獨立同分布的隨機變數在 N → ∞ 時，可以很小的信息損失風險壓縮成多於 N H(X) bit；但相反地，若壓縮到少於 NH(X) bit，則信息幾乎一定會丟失。令 ， 表示兩個有限編碼表，並令 和 （分別）表示來自那些編碼表的所有有限字的集合。設 X 為從 取值的隨機變數，令 f 為從 到 的可解碼，其中 = a。令 S 表示字長 f (X) 給出的隨機變數。
如果 f 是對 X 擁有最小期望字長的最佳碼，那么(Shannon 1948)：
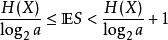信源編碼定理證明
信源編碼定理
信源編碼定理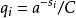
信源編碼定理
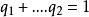信源編碼定理對於 1 ≤ i ≤ n 令 表示每個可能的 的字長。定義 ，其中 C 會使得 。於是
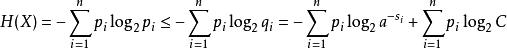信源編碼定理
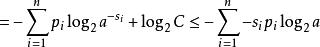信源編碼定理
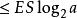信源編碼定理其中第二行由吉布斯不等式推出，而第五行由克拉夫特不等式推出：
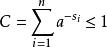信源編碼定理對第二個不等式我們可以令
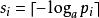信源編碼定理於是：
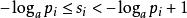信源編碼定理因此
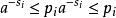信源編碼定理並且
因此由克拉夫特不等式，存在一種有這些字長的無前綴編碼。因此最小的 S 滿足
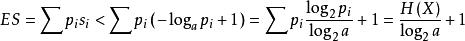信源編碼定理發展
在以大數據為特徵的資訊時代，大量的信息流對信息數據的存儲和傳輸帶來了極大的挑戰。大量的數據直接存儲是高代價且不聰明的做法，信息壓縮存儲往往更加高效。很早以前，工程師們就已經掌握了簡單的壓縮技巧，例如 Huffman 壓縮，複雜度低且效率很高的算數編碼，以及通用的信源編碼算法，像常用的 Lempel-Ziv 算法。然而，由於很多數據之間存在關聯性，另外多信源情形下數據的分散式特性，使得可能存在更加聰明有效的信息壓縮新技術，通信的網路化特徵也預示著更為複雜的聯合壓縮策略相較於單獨壓縮，是更好的選擇。所有這些，也迫切要求相應的信源編碼理論得到不斷發展，以提供理論支持。
美國數學家及工程師 C. E. Shannon在 1948 年發表了題為《A Mathematical Theory of Communication》的學術論文。在該論文中，他提出了通信的數學模型，從信息的抽象概念、信息的度量、壓縮與傳輸等方面建立了一整套相對完整的通信數學理論。在這篇論文中，
Shannon 首次給出了著名的信源編碼定理與信道編碼定理這兩大編碼定理，奠定了一門嶄新的學科，即資訊理論的基礎，宣告了資訊時代的到來。資訊理論作為一門關於通信基本理論的學科，自開創以來，指導了各種信息新技術的發展並指明了可以繼續改進的方向，為資訊時代的進步提供了最為根本的理論依據。Shannon 把所有可以產生信息的源端，比如聲源、光源等抽象為“信源”，以一個機率空間p ，作為其數學表示。為了解決如何有效表示以及有效存儲信息的問題，Shannon 在進行了深入的研究以後，最終給出了信源編碼定理。該定理以一個簡潔漂亮的數學量，即信源的信源熵 H，作為一個信源可以被無損壓縮的理論下界。他在 1959 年發表的另一篇論文中，討論了率失真問題，提出了率失真編碼定理，豐富了信源編碼理論。信源編碼理論的另一個突破來自兩位貝爾實驗室的研究人員，D. Slepian 和J. Wolf， 他們在 1973 年解決了分散式相關信源編碼問題。分散式是通信網路的一個重要特徵，一個關於分散式的理論無疑會對工程套用產生積極的推動和指導作用。自此之後，對於各種模型的多用戶信源編碼問題的研究得到了快速的發展，取得了大量的研究成果。然而，儘管有不少重大的突破和十分漂亮的結果，信源編碼理論還遠不是一個完整的理論，甚至於已解決的問題遠遠少於未解決的問題。自 Slepian 和 Wolf 發表他們里程碑式的論文以後，30 多年過去了。但是後續絕大部分關於多信源編碼問題考慮的是序列編碼情形，關於無錯變長多信源編碼問題研究的相對少得多，這一理論需要得到發展。大多數學者在證明
Shannon 信源、信道編碼定理，以及各種網路編碼定理時，一般都使用隨機編碼技術與典型、聯合典型等數學工具，得出了信源漸進無損壓縮或限失真時的理論下限和信息漸進無錯傳輸的理論上限（描述為各種 Shannon 信息量）。
然而，漸進可忽略的錯誤需要在編碼長度非常大時才能獲得，所以隨機編碼技術並不能直接拿來套用。另外，如果要求接收端知道信源壓縮前的準確信息而不會出錯，那么上述隨機編碼技術就沒有作用了。由於無錯誤的資訊理論問題與組合、圖論中的很多問題有密切的聯繫，比如 Shannon 著名的無錯信道容量問題就可以描述為求一個 n次乘積圖的獨立頂點個數，以及兩維 Kraft 不等式與相關信源特徵圖中最大團（clique）的個數的關係，以及其他一些原因，使得無錯信息理論得到了科研工作者的重視，這一理論也逐漸發展成為資訊理論的一大研究分支。從任意小的漸進和忽略的錯誤機率到完全沒有錯誤，似乎並不是很大的跳躍。然而事實情況是，這兩種情形是截然不同的問題，解決各自問題的方法和工具也完全不相同。
許多研究人員對無錯信源編碼理論進行了討論，提出了解決這一類問題的主要數學工具和手段，尤其是 J. Korner 結合圖理論提出的圖熵概念以及R. Ahlswede 的超圖染色方法，對後續研究具有很大的啟示作用。實現無錯的編碼方案有很多種，本文主要關注採用變長編碼的方法。Shannon 的經典信源編碼定理髮表以後，很快 D. Huffman給出了最小開銷碼構造的 Huffman 編碼程式。我們知道對於機率分布已知的單信源，Huffman 編碼將給出前綴碼，通過觀察輸出碼字序列，可以還原原始信源訊息。作為前綴碼存在的充分和必要條件的 Kraft 不等式首先由 Mc Millan給予證明，隨後 Karush給出了更為常用證明方法。可解碼是比前綴碼更廣泛的一類碼，檢驗其可譯性的Sardinas-Patterson 程式由 A. Sardinas 和 G. W. Patterson在 1956 年給出 。
信源編碼
為減小信源冗餘度而對信源符號進行變換的方法。根據信源性質分類，有信源統計特性已知或未知、無失真或限失真、無記憶或有記憶信源的編碼;按編碼方法分類，有分組碼或非分組碼、等長碼或變長碼等。最常見的是信源統計特性已知的離散、平穩、無失真信源編碼。主要方法有：①統計編碼，如仙農碼、費諾碼、赫夫曼碼、算術碼等。②預測編碼。③變換編碼，以及上述方法的組合(混合編碼)。對於信源統計特性未知的信源編碼稱為通用編碼。衡量信源編碼的主要指標是壓縮比。在無失真編碼中，壓縮的極限是編碼的平均碼錶等於信源的符號熵。在限失真編碼中，冗餘度的壓縮極限與平均失真的關係服從信源的信息率失真R(D)函式。在工程套用中則是在壓縮比，平均失真和工程實現之間尋求折中 。
