定義
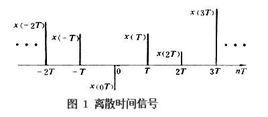
在時間上依次出現的數值序列,例如，{…，0.5，1，2，-1，0，5，…}。相鄰兩個數之間的時間間隔可以是相等的，也可以是不等的。在前一情況下，設時間間隔為 T秒,則離散信號可用符號 x( n T)來表示（圖1）。在間隔 T歸一化為1的條件下, T可以省略,即將 x( n T)表示為 x( n)。 x( n)既可表示整個序列, 也可表示離散信號在 n T瞬間的值。
抽樣
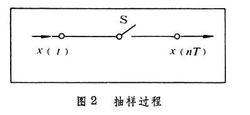圖2
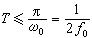間隔T 必須滿足(1)式離散信號可以由連續時間信號抽樣得到。抽樣過程可用圖2來說明。在圖2中開關每隔 T秒閉合,則輸出信號就是離散時間信號 x( t)。間隔時間的長短決定抽樣的離散時間信號能否唯一地表示連續時間信號。抽樣定理指出：一個有限頻譜的連續時間信號 x( t)，如果其頻譜只含有 ω0以下的角頻率分量,則信號 x( t)可以用等間隔的抽樣值來唯一地表示的條件是，間隔 T必須滿足下述關係：(1)式 抽樣間隔 T的倒數稱為抽樣頻率，用 fs表示。從(1)式可見：最低的抽樣頻率應該是連續時間信號 x( t)中最高頻率分量的兩倍。這個最低的抽樣頻率 fs=2 f0通常稱為奈奎斯特抽樣率。
在理論分析和實際套用中，經常遇到兩種典型的離散信號，即單位抽樣信號和離散單位階躍信號。
單位抽樣信號
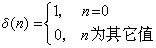(2)或稱離散衝激信號，其定義為 (2)
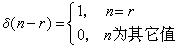因此還應有(3)由於只有單位抽樣信號的宗量等於零時，該信號才能取1的值，因此還應有 (3)
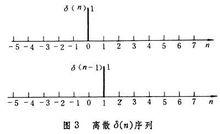圖3δ( n)和 δ( n-1)的序列形式如圖3。
離散單位階躍信號
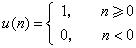離散單位階躍信號(4)它的定義為 (4)
上述兩種典型離散信號序列的關係為
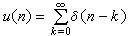兩種典型離散信號序列的關係δ(n)=u(n)-u(n)-(n-1)和 離散時間信號的自變數（時間）是離散的，但其幅度是連續可變的。如果幅度經過量化編碼，則成為數位訊號序列。
