定義
若 ƒ( t)為實數 t的實數函式或是複變函數， t可以為任意實數，則雙邊拉普拉斯變換可以用以下的積分表示：
雙邊拉普拉斯變換此積分為反常積分，此積分收斂若且唯若以下二個積分都存在：
雙邊拉普拉斯變換上述F(s)在s的的某一區域內收斂（即小於無窮大），則由此積分確定的函式稱為f(t)的雙邊拉普拉斯變換，或稱為f(t)的象函式 。而稱f(t)為F(s)的原函式。
使得F(s)收斂的s的取值範圍稱為拉氏變換的收斂域。
註：在給出某函式的雙邊拉氏變換時必須註明其收斂域。
優點
信號不必限制在範圍t>0內，在某些情況下把所研究的問題從時間負無窮到正無窮上作統一考慮，可使概念更清楚。
雙邊拉氏變換與傅立葉變換的聯繫密切，便於全面理解傅氏變換，拉氏變換及Z變換的關係。
1.信號不必限制在範圍t>0內，在某些情況下把所研究的問題從時間負無窮到正無窮上作統一考慮，可使概念更清楚。
2.雙邊拉氏變換與傅立葉變換的聯繫密切，便於全面理解傅氏變換，拉氏變換及Z變換的關係。
與傅氏變換的關係
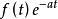雙邊拉普拉斯變換f(t)的雙邊拉普拉斯變換其實就是 的傅氏變換。如果雙邊拉普拉斯變換式的收斂域包括虛軸在內，則把F(s)中的s代換成jw就得到f(t)的傅氏變換，即有：
雙邊拉普拉斯變換故可以把傅氏變換看成雙邊拉氏變換的特例，或雙邊拉氏變換是傅氏變換的推廣 。
性質
1.線性。
雙邊拉普拉斯變換若有： ,
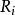雙邊拉普拉斯變換其收斂域為
雙邊拉普拉斯變換 雙邊拉普拉斯變換則有：
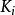雙邊拉普拉斯變換 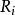雙邊拉普拉斯變換其中 為常數，可為實數也可為複數，收斂域R一般取 的重疊部分，也有可能擴大，若無重疊部分，此性質不成立。該性質利用拉氏正變換性質即可得 。
2.延時(時移特性)
雙邊拉普拉斯變換若有： 則有：
雙邊拉普拉斯變換
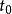雙邊拉普拉斯變換其中 可正可負，收斂域不變 。
3.s域平移
雙邊拉普拉斯變換若有 ,其收斂域為R，則有：
雙邊拉普拉斯變換
雙邊拉普拉斯變換其收斂域為 ，其中Re{-a}表示取-a的實部 。
