歷史
1925年,Ronald Fisher在他1925年的著名書籍 “研究工作者統計方法”(第7章和第8章)中提到了 雙向方差分析。1934年,弗蘭克耶茨發布了不平衡案件的程式。從那時起,已經產生了大量的文獻。這個話題在1993年由Yasunori Fujikoshi審查。2005年,安德魯Gelman提出了一種不同的ANOVA方法,被視為一種多級模型。
數據集
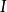 雙向方差分析
雙向方差分析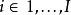 雙向方差分析
雙向方差分析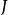 雙向方差分析
雙向方差分析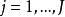 雙向方差分析
雙向方差分析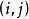 雙向方差分析
雙向方差分析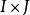 雙向方差分析
雙向方差分析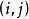 雙向方差分析
雙向方差分析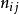 雙向方差分析
雙向方差分析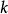 雙向方差分析
雙向方差分析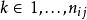 雙向方差分析
雙向方差分析想像一個數據集,其中一個因變數可能受到兩個潛在變異因素的影響。第一個因素有 水平( )和第二個\ 水平( )。每個組合 定義一種治療方法,總共為 治療。我們代表治療的 重複次數 通過 , 然後讓 作為該處理中重複的指標( )。
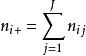 雙向方差分析
雙向方差分析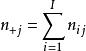 雙向方差分析
雙向方差分析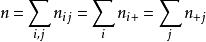 雙向方差分析
雙向方差分析從這些數據中,可以建立一個應急表,其中, 和 ,並且重複的總數等於 。
 雙向方差分析
雙向方差分析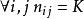 雙向方差分析
雙向方差分析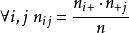 雙向方差分析
雙向方差分析該實驗設計是平衡的,如果每次治療具有相同數量的重複的, 。在這種情況下,設計也被認為是正交的,從而可以完全區分這兩種因素的影響。因此我們可以寫 和 。
模型
 雙向方差分析
雙向方差分析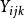 雙向方差分析
雙向方差分析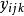 雙向方差分析
雙向方差分析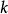 雙向方差分析
雙向方差分析 雙向方差分析
雙向方差分析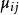 雙向方差分析
雙向方差分析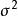 雙向方差分析
雙向方差分析一旦觀察到變異數據點 ,例如通過直方圖,“機率可能被用來描述這種變化”。因此讓我們表示 觀察值的隨機變數 是第 個治療措施 。該雙向方差分析模型中的所有這些變數變化的獨立和通常圍繞一個平均值 ,具有不變的方差 :
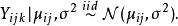 雙向方差分析
雙向方差分析具體而言,回響變數的均值被建模為解釋變數的線性組合:
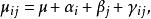 雙向方差分析
雙向方差分析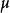 雙向方差分析
雙向方差分析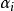 雙向方差分析
雙向方差分析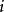 雙向方差分析
雙向方差分析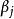 雙向方差分析
雙向方差分析 雙向方差分析
雙向方差分析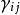 雙向方差分析
雙向方差分析 雙向方差分析
雙向方差分析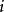 雙向方差分析
雙向方差分析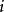 雙向方差分析
雙向方差分析 雙向方差分析
雙向方差分析這裡 表示總平均, 是等級的附加主效應 從第一個因素(第一個在contigency表中的行), 是等級的附加主效應 從第二個因素(第j個列在contigency表)和 是治療的非加性相互作用效應 來自這兩個因素(第 行第 列和第 列在contigency表中)。
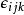 雙向方差分析
雙向方差分析 雙向方差分析
雙向方差分析描述雙因素方差分析的另一種等效方法是提及除了因素解釋的變化之外,還存在一些統計噪音。通過在每個數據點引入一個隨機變數來處理這種未解釋的變化量, ,稱為錯誤。這些 隨機變數被視為與平均數的偏差,並被假定為獨立常態分配:
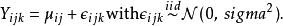 雙向方差分析
雙向方差分析假設
在Gelman和Hill之後,ANOVA的假設以及更一般的一般線性模型按重要性遞減順序 :
1)數據點與調查中的科學問題有關;
2)回響變數的平均值受累加性影響(如果不是相互作用項),並且受到因素的線性影響;
3)錯誤是獨立的;
4)錯誤具有相同的方差;
5)錯誤是常態分配的。
參數估計
為了確保參數的可識別性,我們可以添加下面的“總和到零”約束:
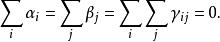 雙向方差分析
雙向方差分析