定義
集族(family of sets)是由具有某種性質的一些集合所構成的集合,即“集合的集合”。例如,平面上的圓盤是集合,因此平面上一切圓盤所成的集合就是一個集族。又如一個集合的一切子集所構成的集合也是一個集族。
 集族
集族 集族
集族 集族
集族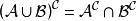 集族
集族集族是以集合為元素構成的集合。集族常用花體字母表示,這裡我們使用 來表示集族。集合之間關係的定義和運算規律同樣適用於集族。如 為集族 的可列並, 。
幾種常用集族
下面我們介紹幾種常用的集族。
| 集族類別 | 等價定義 | 對運算的特性 |
| 半環 | 對交封閉,差為有限不相交並 | |
| 環 | 對“U”“\”封閉 對“U”“△”封閉 對“∩”“△”封閉 對“∩”,不相交並,包含差封閉 | 對一切有限 運算封閉 |
| 代數 | 含X的環 對“U” 余“ ' ’”封閉 對“∩” 余“ ' ’”封閉 | 含X且對一切有 限運算封閉 |
| σ-代數 | 對 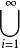 集族 集族 | 含X且對一切可 列運算封閉 |
半環
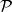 集族
集族定義1 設 為一集族,且滿足下列三個條件。
 集族
集族1)
 集族
集族 集族
集族2) 若 ,則
 集族
集族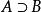 集族
集族3) 若 且 則
 集族
集族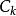 集族
集族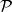 集族
集族 集族
集族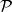 集族
集族其中每一個 均屬於 且 則稱 為 半環 。
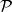 集族
集族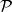 集族
集族 集族
集族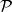 集族
集族顯然若 為半環,那么 中任二元素A,B之差 必能表為 中有限個兩兩不相交的集之並。
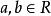 集族
集族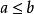 集族
集族例1 記全體實數所成的集為R; 且 ,那么我
們把集
 集族
集族稱為R中的 左閉右開區間,簡稱半開閉區間,R中全體半開區間構成一個半環。
例2 設R 為n維實數空間(即n維歐幾里得空間),又設
 集族
集族 集族
集族 集族
集族為 中兩元素且 那么 Rn滿足下列關係
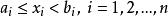 集族
集族 集族
集族的元素 所組成的集稱為R 中的半開閉區間。
R 中全體半開閉區間構成一個半環。
 集族
集族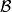 集族
集族 集族
集族 集族
集族例3 設X為任意集,用 (X)表示X中全體子集組成的集族,則 (X)為半環,只含 集的集族{ }亦是一個半環。
 集族
集族例4 設X為任意集,X中全體單點集連同 集構成一個半環。
環
 集族
集族 集族
集族 集族
集族 集族
集族定義2 設 為不空集族,且滿足下述條件:若 ,則 ,那么我們稱 為 環.換句話說:如果一個非空集族對於並及差兩種運算是封閉的,那么它就是一個環。
例3中的集族也是環。
例5 設X是無窮集,則由X中一切有限子集組成的集族是環。
容易證明, 凡環必是半環,反之半環不一定是環.上面例1,例2及例4中的集族均是半環,但它們都不是環。
 集族
集族 集族
集族定理1 設 為不空集族,則下列1) 2) 3)都是使 為環的充要條件:
 集族
集族 集族
集族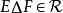 集族
集族1) 若 ,則 , ;
 集族
集族 集族
集族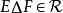 集族
集族2) 若 ,則 , ;
 集族
集族 集族
集族3) 若 ,則 ,
 集族
集族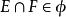 集族
集族 集族
集族若 且 ,則 ,
 集族
集族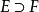 集族
集族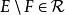 集族
集族若 且 ,則 。
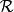 集族
集族 集族
集族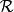 集族
集族推論1 若 為環,則 且 對有限個集之並,交及兩集之差,對稱差運算封閉。
代數
定義3 含X的環稱為代數,由定理1的推論及
 集族
集族可知:代數對於有限個集之並及交,兩集之差及對稱差,余集等運算是封閉的。
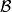 集族
集族顯然例3中的集族 (X)是代數。
倒6 設X是無窮集,X中全體有限子集及余集是有限集的集所組成的集族是一個代數。
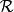 集族
集族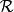 集族
集族顯然代數是環,反之環未必是代數,而且若 是環,那么由X和 中的集組成的集族也未必是代數.事實上例5中的集族是環但非代數,而且該集族增添元素X後所得的集族也不是一個代數,因為它對余運算不封閉。
 集族
集族定理2 設 為不空集族,則下列命題等價:
 集族
集族1) 含X的環;
 集族
集族 集族
集族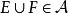 集族
集族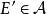 集族
集族2) 對並及余運算封閉,即若 ,則 , ;
 集族
集族 集族
集族 集族
集族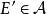 集族
集族3) 對交及余運算封閉,即若 ,則 , 。
σ-代數
 集族
集族定義4假設 是Ω上的非空集族,如果:
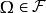 集族
集族(1) ;
 集族
集族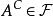 集族
集族(2)它對於補運算封閉,即 ,有 ;
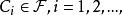 集族
集族 集族
集族(3)它對於可列並運算封閉,即 有 。
 集族
集族 集族
集族則稱 是Ω上的 (西格瑪)-代數(algebra)或者 域(field)。
 集族
集族 集族
集族 集族
集族例7由 Ω和 兩個集合組成的集族是 -代數。因為它們的補和可列並運算結果仍然是Ω和 。
 集族
集族 集族
集族 集族
集族 集族
集族 集族
集族(2)假設A是Ω的非空子集, 是任一包含A的-代數,那么 稱為包含A的最小 -代數,有時也稱為由A生成的-代數。
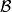 集族
集族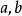 集族
集族 集族
集族 集族
集族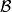 集族
集族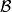 集族
集族(3)設Ω是全體實數R,令是R中一切開區間( )生成的 -代數(一切閉區間也可以),稱為R中的波雷耳(Borel) -代數,記為 (R), 中的元素(集合)稱為R中的波雷耳集。

