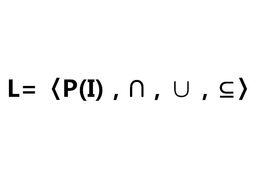基本介紹
一個集合,連同定義在該集合上的一種或多種運算並使它滿足一定的條件,在數學中就被稱為一個代數結構。例如,實數集,連同定義在其上的通常加法與乘法運算,它們滿足一定的關於數的公理,構成的實數系R就是一個代數結構 。
集合代數也是一種具有廣泛套用價值的代數結構。
 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數設S是全集,是S的一些子集組成的子集類,在上定義著並∪、交∩及補一運算,同時滿足:對中任意集合A、B,均有
 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數A∪B∈ 且∈
 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數則稱是一個 集合的布爾代數,簡稱 集合代數。如果對中的任一無限子集⊆亦有
 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數則稱為集合的布爾代數,簡稱σ-代數 。
 集合布爾代數
集合布爾代數很明顯,在這裡“代數”一詞是強調並集運算及補集運算的結果仍在中,具有封閉性。
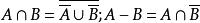 集合布爾代數
集合布爾代數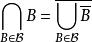 集合布爾代數
集合布爾代數由於以及,所以在集合代數及集合σ-代數中關於交運算及差運算亦是封閉的。
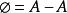 集合布爾代數
集合布爾代數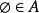 集合布爾代數
集合布爾代數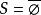 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數另外,由知,;由,S∈。
 集合布爾代數
集合布爾代數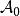 集合布爾代數
集合布爾代數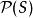 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數由一個給定的全集S,可以構成許多集代數,按定義容易驗證:僅有∅及S組成的子集類={∅,S}是最小的集合代數;S的冪集是最大的集合代數。如果是任一個集合代數,則必有
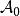 集合布爾代數
集合布爾代數 集合布爾代數
集合布爾代數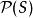 集合布爾代數
集合布爾代數⊆⊆.
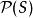 集合布爾代數
集合布爾代數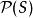 集合布爾代數
集合布爾代數由於當全集S(被研究對象的全體)被明確後,其冪集可自然構成一個集合代數,所以在大多數初等套用中,特別是在實際套用中多半使用,而且經常不加說明 。
例題解析
【例1】設某計算機全部記憶體分配成四個區域:系統區,第一道作業專用區,第二道作業專業區,第三道作業專用區以及這些作業的公共區,試用集合代數方法描述第二道作業不能訪問的記憶體區 。
解 全集S應當是要研究的全部記憶體單元,若令A表示系統區記憶體區域;A(i=1,2,3)表示第i道作業專用區域;C表示作業共用記憶體區域,則第二道作業記憶體區域為
A∪C.
於是,第二道作業不能訪問區為
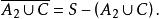 集合布爾代數
集合布爾代數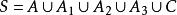 集合布爾代數
集合布爾代數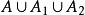 集合布爾代數
集合布爾代數又由
,且記憶體分配區間不能重疊,所求區域亦可表示為(試證之)。
【例2】某圖書館藏各類圖書100萬冊,一讀者想收集該館以描寫校園生活為題材的長篇小說以及九十年代出版的非歷史題材的長篇小說目錄,試用集合論方法描述該目錄。
解 在此問題中,全集S為該館全部藏書之書名組成的集合,今若令:
R:所有長篇小說書名目錄;
H:所有以校園生活為題材的書名目錄;
L:所有九十年代出版的書名目錄;
K:所有歷史題材的書名目錄.
則該讀者所需收集之書名目錄可表示成 :
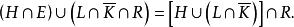 集合布爾代數
集合布爾代數集合代數
集合代數(set algebra)亦稱冪集代數,是一種特殊的集合族的代數,如果集族A的元素對於指定的某些集合運算封閉,這些運算滿足若干公理,就稱集族A關於這些運算在指定公理體系下成為一個集合代數。例如,集合環、集合域等都是集合代數,這裡A稱為這個集合代數的基礎集(族),這些運算稱為集合代數的運算 。
常見的集合代數如下:
1.對於集合的並運算封閉的集族A作成的並代數:〈A,∪〉.
2.對於集合的交運算封閉的集族A作成的交代數:〈A,∩〉.
3.集合環:〈A,∩,∪〉.
4.集合域:〈A,∩,∪,﹣〉.
5.以全集I的冪集P(I)為基礎集的集合代數:〈P(I),∩,∪,С〉,“С”表示集合的補運算,這種集合代數是一種布爾代數。
集合代數與其他代數不同之點是:
1.它以集族為基礎集合。
2.它的運算是集合運算。
3.它的公理體系就是在集合運算的基本性質上添上或不添上若干附加要求 。