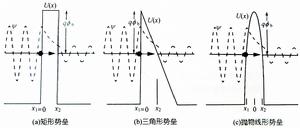
 三種典型量子勢壘的隧穿
三種典型量子勢壘的隧穿對於有限高度的勢壘,當勢壘厚度與微觀粒子的de Broglie波長接近時,則對於微觀粒子來說,該勢壘就是量子勢壘;因為這時的微觀粒子可以利用其波動性而直接穿過勢壘,即隧道效應。若微觀粒子是電子,那么電子隧穿量子勢壘即將產生隧穿電流。
如果知道了電子發生量子隧穿的幾率T,則隧穿電流密度j可以求出為(設電子濃度為n,電子的熱運動速度為vth): j = -q n vth T
(2)不同形狀勢壘的隧穿幾率T:
在圖1中示出了三種典型的勢壘;有效勢壘寬度為x1~x2。
決定電子波函式的Schrodinger方程為: d2Ψ/dx2 + (2m*/ħ2) [E-U(x)] Ψ = 0
如果式中的電勢能U(x)變化不很快,則該方程可以採用WKB近似來簡化,並可求出隧穿前後兩邊波函式之比為: |Ψ(x2)| / |Ψ(x1)| = exp{- ∫ [(2m*/ħ2)(U(x)-E)]1/2 dx} (積分限為x1~x2)
可見,在勢壘區內,波函式是指數式衰減的;這是由於在此U(x)>E(動能為負),則波矢為虛數,即k=i[(2m*/ħ2)(U(x)-E)]1/2,從而,上面的波函式之比可變形為exp{-|k|x}。在勢壘區以外的1區和2區都是平面波(在2區是波幅較小的平面波),波矢都是實數,即k=(2m*E/ħ2)1/2。
因為電子出現的幾率∝|Ψ|2,所以,根據上面的結果可求得電子的隧穿幾率為
T = |Ψ(x2)|2 / |Ψ(x1)|2 = exp{-2 ∫ [(2m*/ħ2)(U(x)-E)]1/2 dx} (積分限為x1~x2)
顯然,勢能U(x)的形式不同,即不同形狀的勢壘,則電子的隧穿幾率也就不同。
對於矩形勢壘(圖1(a)),電子的勢能U(x) = q Φb =常數(即勢壘高度恆定),則電子的隧穿幾率為
T(矩形)= exp[-2(2m* qΦb/ħ2)1/2 Δx]
對於三角形勢壘(圖1(b)),電子的勢能線性變化,即U(x)-E = qΦb (1-x/Δx),則有隧穿幾率:
T(三角形)= exp[-(4/3) (2m* qΦb/ħ2) Δx] = exp [ -4 (2m*q)1/2(Φb)3/2 / (3ħ|E|) ]
式中的E是勢壘中的電場強度。
對於拋物線形勢壘(圖1(c)),U(x)-E = q Φb (1-4x/Δx),則有隧穿幾率:
T(拋物線)= exp[-(p/2) (2m*qΦb/ħ2)1/2 Δx]
(3)MIS的隧穿電流:
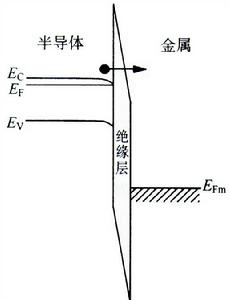 圖2,MIS的隧道效應
圖2,MIS的隧道效應j = -q n vth T(三角形) = C1 E2 exp(C2/E)
其中的常數C1=9.625×10,C2=2.765×10V/cm。
特別,對於MOS系統,電子從Si隧穿二氧化矽的勢壘可近似為斜頂梯形的勢壘,這種隧穿往往稱為直接隧穿。
