規範場論
規範場論(Gauge Theory)是基於對稱變換可以局部也可以全局地施行這一思想的一類物理理論。非交換對稱群(又稱非阿貝爾群)的規範場論最常見的例子為楊-米爾斯理論。物理系統往往用在某種變換下不變的拉格朗日量表述,當變換在每一時空點同時施行,它們有全局對稱性。規範場論推廣了這一思想,它要求拉格朗日量必須也有局部對稱性—應該可以在時空的特定區域施行這些對稱變換而不影響到另外一個區域。這個要求是廣義相對論的等效原理的一個推廣。
規範“對稱性”反映了系統表述的一個冗餘性。
規範場論在物理學上的重要性,在於其成功為量子電動力學、弱相互作用和強相互作用提供了一個統一的數學形式化架構——標準模型。這套理論精確地表述了自然界的三種基本力的實驗預測,它是一個規範群為SU(3) × SU(2) × U(1)的 規範場論。像弦論這樣的現代理論,以及廣義相對論的一些表述,都是某種意義上的規範場論。
有時,規範對稱性一詞被用於更廣泛的含義,包括任何局部對稱性,例如微分同胚。該術語的這個含義 不在本條目使用。
規範場論簡史
最早包含規範對稱性的物理理論是詹姆斯·麥克斯韋的電動力學。麥克斯韋在他的論文裡特別提出,這理論源自於開爾文男爵於1851年發現的關於磁矢勢的數學性質。但是,該對稱性的重要性在早期的表述中沒有被注意到。大衛·希爾伯特假設在坐標變換下作用量不變,由此推導出愛因斯坦場方程時,但它也沒有注意到對稱性的重要。之後,赫爾曼·外爾試圖統一廣義相對論和電磁學,他猜想“Eichinvarianz”或者說尺度(“規範”)變換下的“不變性”可能也是廣義相對論的局部對稱性。後來發現該猜想將導致某些非物理的結果。但是在量子力學發展以後,外爾、弗拉基米爾·福克和弗里茨·倫敦實現了該思想,但作了一些修改(把縮放因子用一個複數代替,並把尺度變化變成了相位變化—一個U(1)規範對稱性),這相應於帶電荷的量子粒子其波函式受到電磁場的影響,給定了一個漂亮的解釋。這是第一個規範場論。泡利在1940年推動了該理論的傳播。
1954年,為了解決一些基本粒子物理中的巨大混亂,楊振寧和羅伯特·米爾斯引入非交換規範場論,來建構將核子綁在原子核中的強相互作用的模型。(Ronald Shaw,在阿卜杜勒·薩拉姆指導下,在他的博士論文中獨立地引入了相同的概念。)通過推廣電磁學中的規範不變性,他們試圖構造基於(非交換的)SU(2)對稱群在同位旋質子和中子對上的作用的理論,類似於U(1)群在量子電動力學的旋量場上的作用。在粒子物理中,重點在於 量子化規範場論。
該思想後來被發現能夠用於弱相互作用的量子場論,以及它和電磁學的電弱統一理論中。當人們意識到非交換規範場論能夠導出漸近自由的時候,規範場論變得更有吸引力,因為漸近自由被認為是強相互作用的一個重要特點—因而推動了尋找強相互作用的規範場論的研究。這個理論現在稱為量子色動力學,是一個SU(3)群作用在夸克的色荷上的規範場論。標準模型用規範場論的語言統一了電磁力、弱相互作用和強相互作用的表述。
1970年代麥可·阿蒂亞爵士提出了研究 經典楊-米爾斯方程的數學解的計畫。1983年,阿蒂亞的學生西蒙·唐納森在這個工作之上證明了光滑4-流形的可微性分類和同胚性分類非常不同。麥可·弗里德曼採用唐納森的工作證明奇異 R的存在,也就是,歐幾里得4維空間上的奇異微分結構。這導致對於規範場論作為數學理論的興趣逐漸增加,獨立於它在基礎物理中的成功。1994年,愛德華·威滕和Nathan Seiberg發明了基於超對稱的規範場技術,使得特定拓撲不變數的計算成為可能。這些數學上的成果也導致了對該領域的新興趣。
電磁學中的簡單的規範對稱性的例子
電路中接地的定義是規範對稱性的一個例子;當線路所有點的電位升高相同的值時,電路的行為完全不變;因為電路中的電位差不變。該事實的一個常見釋例是棲息在高壓電線上的鳥不會遭電擊,因為鳥對地絕緣。
這稱為整體規範對稱性。電壓的絕對值不是真實的;真正影響電路的是電路組件兩端的電壓差。接地點的定義是任意的,但一旦該點確定了,則該定義必須全局的採用。
相反,如果某個對稱性可以從一點到另一點任意的定義,它是一個局域規範對稱性。
阿貝爾範疇
定義
阿貝爾範疇的公理版本繁多,在此僅取其一(見外部連結)。
 阿貝爾規範場論
阿貝爾規範場論一個範疇 若滿足下述條件,則稱 阿貝爾範疇:
1.是加法範疇。
2.所有態射皆有核與上核。
3.所有態射皆為嚴格態射。
 阿貝爾規範場論
阿貝爾規範場論只滿足前兩個條件者稱作 預阿貝爾範疇。
若取k為一交換環,則在上述定義中以k-加法範疇代換加法範疇,便得到k-阿貝爾範疇之定義。
基本性質
在阿貝爾範疇中,任何態射f皆可分解為單射。滿射,其中的滿射稱為f的上像,而單射則稱為f的像。此性質源自公理中對態射嚴格性的要求。
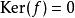 阿貝爾規範場論
阿貝爾規範場論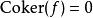 阿貝爾規範場論
阿貝爾規範場論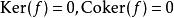 阿貝爾規範場論
阿貝爾規範場論任一態射f是單射若且唯若 ,是滿射若且唯若 ,是同構若且唯若 。
子對象與商對象具良好性質。例如:任一對象的子對象構成的偏序集合是有界格。
 阿貝爾規範場論
阿貝爾規範場論任一阿貝爾範疇 可構想為有限生成阿貝爾群的么半範疇上的模;這意謂著我們能構造一個有限生成阿貝爾群G與對象A的張量積。
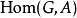 阿貝爾規範場論
阿貝爾規範場論 阿貝爾規範場論
阿貝爾規範場論 阿貝爾規範場論
阿貝爾規範場論承上,阿貝爾範疇也是上模; 可以詮釋為 的對象。若 完備,G的有限生成假設可以移除。
相關概念
阿貝爾範疇是同調代數的基本框架,它容許討論同調代數中的基本構造,如正合序列、短正合序列與導函子。
對所有阿貝爾範疇均成立的重要結果包括五引理(含特例短五引理)與蛇引理(含特例九引理)等等。
