基本介紹
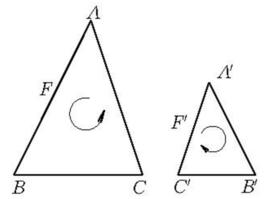
鏡像相似是一種特殊相似形,設圖形F與F′是相似形,在圖形F上任取不共線的三點A,B,C,它們在圖形F′上的對應點分別是A′,B′,C′(如圖1),若△ABC與△A′B′C′的方向相反,例如,沿周界ABCA的環繞方向與沿周界A′B′C′A′的環繞方向一個為逆時針方向,而另一個為順時針方向,則稱圖形F與圖形F′ 鏡像相似。鏡像相似圖形的重要特例是鏡像相似三角形。設△ABC與△A′B′C′相似,且沿周界ABCA及A′B′C′A′環繞方向相反,若一個為逆時針方向,另一個為順時針方向,則這兩個三角形是鏡像相似三角形 。
 圖1
圖1相關結論
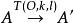 鏡像相似
鏡像相似定理1 設T(O, k, l)(k≠1)是平面π的一個位似軸反射變換,A是平面π上不在其反射軸上的任一點,且,直線AA’與內反射軸l交於P,與外反射軸m交於Q,則
 鏡像相似
鏡像相似定理2位似軸反射變換是鏡像相似變換 。
證明: 因位似軸反射變換是軸反射變換與位似變換之積,軸反射變換是鏡像契約變換(當然也是鏡像相似變換),位似變換是真正相似變換,而鏡像相似變換與真正相似變換之積是鏡像相似變換,故位似軸反射變換是鏡像相似變換。
位似軸反射變換儘管是兩個已知變換——軸反射變換與位似變換的乘積,但它有一個不動點——位似軸反射中心,更重要的是有下面的定理。
定理3 相似係數不等於1的鏡像相似變換必為位似軸反射變換。
由於位似中心是位似軸反射變換(只要位似係數不等於1)的唯一的不動點,因而由定理3即知,相似係數不等於1的鏡像相似變換必有唯一的不動點。
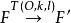 鏡像相似
鏡像相似如果平面π上的兩個圖形F與F'鏡像相似,且相似係數不等於1,則由定理3,存在平面π的一個位似軸反射變換T(O, k, l),使得 ,這時,位似中心O稱為圖形F與F'的逆相似中心,而反射軸(內、外兩條)則稱為圖形F與F'的相似軸。
只有鏡像相似圖形(相似比不等於1)才有相似軸,順相似中心與逆相似中心統稱為相似中心。
對於平面上的兩個相似圖形,只要其相似係數不等於1,它們就有一個相似中心。
當兩個圖形鏡像相似(相似比不等於1)時,如何作出其相似軸和相似中心?實際上,定理1已經告訴了我們作法,
如圖2所示,設A、B兩點在位似軸反射變換T(O,k, l)下的像點分別為A'、B',以相似比k分別內分和外分線段A'A與B'B,則兩個內分點M、N的連線及兩個外分點P、Q的連線即為兩條相似軸,而兩相似軸的交點O即為相似中心。
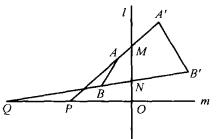 圖2
圖2站在相似軸與相似中心的平台上看某些平面幾何問題,會顯得十分簡單 。
例題解析
【例1】設△ABC與△A'B'C'鏡像相似,相似比不等於1,以相似比為分比內分線段A'A、B'B、C'C於D、E、F;再以相似比為分比外分線段A'A、B'B、C'C於P、Q、R。求證: D、E、F 三點與P、Q、R三點分別共線,且這兩條直線互相垂直。
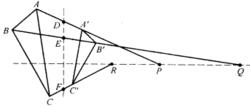 圖3
圖3證明 如圖3所示,因△ABC與△A'B'C'鏡像相似,且相似比不等於1,所以,它們有兩條互相垂直的相似軸。由定理知,D、E、F與P、Q、R分別位於兩條相似軸上,故結論成立。
【例2】設△ABC與△A'B'C'真正相似,相似比為k,以k為分比分別內分線段C'B、B'C、A'C、C'A、B'A、A'B於點I、J、K、L、M、N,則IJ、KL、MN三線共點。
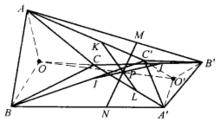 圖4
圖4證明 如圖4,設O、O'分別是△ABC和OA'B'C'的外心,則△BOC與△C'O'B'是鏡像相似的。以k為分比內分線段O'O於P,則由上題知,I、P、J三點是共線的,即IJ通過點P,同理,KL、MN皆通過點P,故IJ、KL、MN三線共點 。