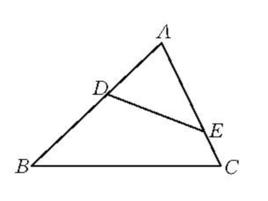
概念
若B'、C'分別是△ABC中AC和AB(所在直線)上的點,△ABC∽△A'B'C'且頂點排列順序方向相反(即為鏡像相似),則稱BC和B'C'為關於∠A的逆平行線。線段B'C'稱為△ABC的邊BC的逆相似邊 。
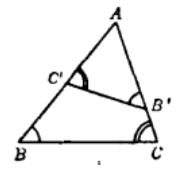 圖1
圖1逆相似邊的性質
逆相似邊有如下性質(圖1):
(1)B、C、B'、C'四點共圓;
(2) 同邊的逆相似邊互相平行;
(3)三角形各邊的逆相似邊與該三角形的外接圓各頂點的切線平行。
逆相似邊與類似中線關係密切,有性質:過三角形的一個頂點而平分對邊的逆相似邊是類似中線。
逆相似邊與陪位中線的性質
陪位中線與逆平行線有如下性質:
在△ABC中,以BC為弦作一圓,與AB、AC交於點C'、B',則∠AB'C'=∠B,就稱B'C'為BC的逆相似邊或逆平行線。在一個三角形中,
(1)同邊的逆平行線平行;
(2)某邊的逆平行線被這邊陪位中線平分;
(3)過頂點平分其對邊逆平行線的直線是陪位中線;
(4)被陪位中線平分的線段必為逆平行線。
證明:(1)結論是明顯的。
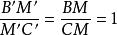 逆相似邊
逆相似邊(2)設M是BC中點,B'C'與BC陪位中線交於點M'(圖略),由△ABC∽△AB'C'及∠BAM =∠B'AM',可得,即M'是B'C'的中點,AM'平分B'C'。
(3)若AM'平分B'C',則有△AB'M'∽△ABM,∠B'AM =∠BAM,即AM'是BC的陪位中線。
(4)設BC的陪位中線平分線段B'C'於點M',若B'C'不是BC的逆平行線,則過B、C、B’作一圓交AB於點C",B'C"是BC的逆平行線,由(2)知B'C"被AM'平分,設中點為M",則M'M"是△B'C'C"的中位線,得M'M"// AB,但AM'與AB相交於點A,矛盾,所以B'C'是BC的逆平行線。
舉例分析
勒穆瓦納圓中的逆相似邊
三角形的第一Lemoine圓 過三角形陪位重心作三邊的平行線與各邊相交的六個交點共圓。
陪位重心:設△ABC的三條中線AM、BN、CL的交點為G(重心),過A作AM'使∠CAM'=∠BAM,作BN'使∠ABN'=∠CBN,作CL'使∠ACL'=∠BCL,則AM'、BN’、CL'三線共點於K,這個點就稱為三角形的陪位重心,AM'、BN'、CL'稱為陪位中線。
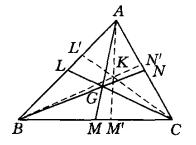 圖2
圖2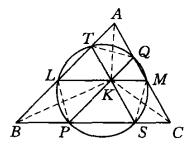 圖3
圖3該圓於1873年為Lemoine所得到。設K為△ABC陪位重心,過K作LM∥BC交AB、AC於L、M,作PQ∥AB交BC、AC於P、Q,作ST∥AC交BC、AB於S、T。
連結TQ、AK,因為四邊形ATKQ是平行四邊形,所以TQ與AK互相平分。因為AK是△ABC的陪位中線,所以過K點的關於BC的逆平行線也被AK平分,故而TQ為關於BC的逆平行線。
於是∠AQT=∠ABC=∠ALM,T、L、M、Q四點共圓。同理可證Q、P、S、M四點共圓,T、L、P、S四點共圓,從而得到T、L、P、S、M、Q六點共圓。
三角形的第二Lemoine圓:過三角形陪位重心作各邊的逆平行線與各邊相交的六個交點共圓。
該圓於1873年為Lemoine所得到。
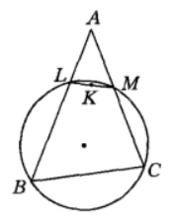 圖4
圖4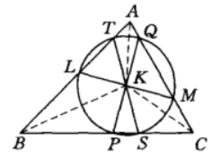 圖5
圖5逆平行線:過△ABC內任一點K,作直線交AB、AC於L、M,使△AML∽△ABC,但LM不平行於BC,則稱ML為過K關於BC的逆平行線。三角形有三類這樣的逆平行線。若K是陪位重心,則K將平分過K的三條逆平行線。
設K是陪位重心,LM、PQ、ST是過K點的逆平行線,因為
∠ALM=∠C,∠AML= ∠B,
∠BST=∠A,∠BTS=∠C,
∠CQP=∠B,∠CPQ=∠A,
所以∠ALM=∠BTS,△KTL是等腰三角形,其兩腰KL= KT。
同理有KP = KS,KM = KQ。
又陪位重心K平分過K點的逆平行線,所以又有KL= KM,KP = KQ,KS = KT。
這樣L、P、S、M、Q、T六點到K點的距離相等,從而這六點共圓。