基本介紹
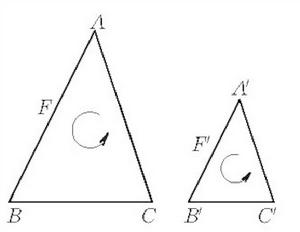
真正相似是一種特殊相似形,設圖形F與F′是相似形,在圖形F上任取不共線 三點A,B,C,它們在圖形F′上的對應點分別是A′,B′,C′(如圖1),若△ABC和△A′B′C′的方向相同,即三對對應點的排列(沿周界ABCA與A′B′C′A′的環繞方向)或同為順時針方向或同為逆時針方向,則稱圖形F與圖形F′真正相似。真正相似圖形的重要特例是真正相似三角形。當△ABC與△A′B′C′相似,且沿周界ABCA與沿周界A′B′C′A′的環繞方向相同,即同為逆時針方向或同為順時針方向,則這兩個三角形是真正相似三角形 。
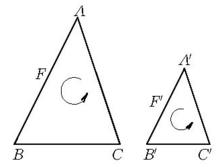 圖1
圖1相關定理
定理1 位似圖形必彼此真正相似 。
定理2 若兩非契約的真正相似圖形有一雙對應直線互相平行或重合,則它們必是位似圖形。
注 必須注意,即使兩真正相似圖形的每雙對應頂點連線共點,但這兩圖形未必是位似的,例如在下圖中所繪的△ABC與△A'B'C',它們不但真正相似,且有透視中心O,然而它們明明就不是位似圖形。
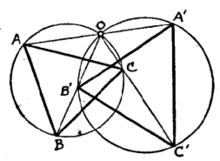 圖2
圖2定理3 既不契約也不位似的兩個真正相似圖形,可以接連行一次位似變換和一次旋轉將其一形變為他形, 其中相似中心和旋轉中心是同一點。
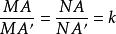 真正相似
真正相似定理4設圖形F與F'真正相似但不契約,A與A'是任一雙對應點,k是相似比。若內外分錢段AA'於M、N,使,則直徑為MN的圓恆過一定點。
定理5 非契約的兩個鏡象相似圖形,可以接連行一 次反射和一次位似變換將其一形變為另一形,其中反射軸通過相似中心。
定理6 非契約的兩個鏡象相似圖形的兩條二重線,內外分每雙對應點的連線線所得的分比,都等於兩形的相似比 。
相關介紹
如果二圖形F和F'的點與點之間建立這樣的一一對應應關係,即圖形F'上任意二點連線而成的線段與圖形F上與前二點對應的二點連線而成的線段的比有同一數值,就說圖形F'相似子圖形F,設A、B、C、D、…為圖形F上的點,圖形F'上的對應點為A'、B'、C'、D'、…,由定義,必有K=A'B':AB=A'C':AC=B'C':BC=A'D':AD…=常數,這個比例常數K稱為圖形F'對於圖形F的相似係數或稱相似比 。
特別地,如果兩個邊數相同的多邊形的對應角都相等,對應邊都成比例,這兩個多邊形叫做相似多邊形。對於兩個三角形,如果對應角相等,對應邊成比例,這兩個三角形叫做相似三角形,相似用符號“∽”表示,讀作“相似於”。
有兩種相似圖形。如果給圖形以定向, 則有
(1)兩相似圖形上的每兩個對應三角形有同一的定向,每兩對應角有同向,這兩個相似圖形稱為真正相似(圖3)。
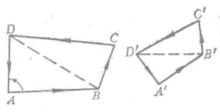 圖3
圖3(2)兩相似圖形上的每兩個對應三角形有相反的定向,每兩對應角有相反方向,這兩個相似圖形稱為鏡象相似(圖4)。
 圖4
圖4