量子震盪

在凝聚態物理學中，量子振盪描述了一系列相關的實驗技術，用於在存在強磁場的情況下映射金屬的費米面。這些技術基於費米子在磁場中運動的朗道量子化原理。對於強磁場中的自由費米子氣體，能級被量化成帶，稱為朗道能級，其分離度與磁場強度成反比。在量子振盪實驗中，外部磁場是變化的，這導致朗道能級通過費米面，從而導致費米能級電子態密度的振盪;這會在許多取決於此的材料屬性中產生振盪，包括阻力（Shubnikov-de Haas效應），霍爾電阻和磁化率（de Haas-van Alphen效應）。觀察材料中的量子振盪被認為是費米液體行為的特徵。 量子振盪已被用於研究高溫超導材料，如銅酸鹽和磷酸鹽。使用這些實驗的研究表明，未摻雜的銅酸鹽的基態與費米液體表現類似，並且顯示出諸如朗道準粒子的特徵。

實驗

當一個磁場被施加到一個自由電荷的費米體系上時，它們的能量狀態被量化成所謂的朗道能級，由：

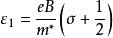量子震盪

量子震盪

量子震盪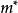

量子震盪

量子震盪

對於整數值 ，其中 是外部磁場， ， 分別是費米子電荷和有效質量。

量子震盪

當外部磁場 在孤立系統中增加時，朗道能級擴展，並最終“消失”費米面。 這導致觀察到的最高占據能級的能量振盪，並因此導致許多物理性質（包括霍爾電導率，電阻率和磁化率）。可以測量這些振盪的周期性，並且可以用來確定費米面的橫截面面積。如果磁場的軸以恆定的幅度變化，則觀察到類似的振盪。無論何時朗道軌道接觸費米表面都會發生振盪。通過這種方式，可以映射費米球的完整幾何。

銅礦

通過探針如ARPES對YBa2Cu3O6 + x等未摻雜的銅酸鹽化合物的研究表明，這些相顯示出非費米液體的特性，特別是沒有明確的Landau準粒子。然而，如果這些材料的超導電性受到足夠高的磁場的抑制，這些材料在低溫下就會觀察到量子振盪，這證明了費米子統計學中存在明確定義的準粒子。這些實驗結果與ARPES和其他探針的結果不一致。

量子振盪的頻率及其物理意義

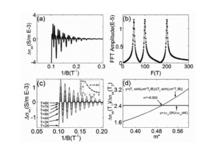圖1

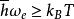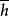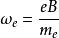量子震盪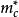

量子震盪

量子震盪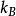

量子震盪

量子震盪

量子震盪

量子震盪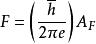

量子震盪

量子震盪

在單晶材料中，當 時,其中 是約化普朗克常量。 為迴旋頻率， 為電子電荷量， 為磁場強度， 為迴旋有效質量， 為玻爾茲曼常數， 為溫度，材料的態密度就會隨磁場變化與磁場的倒數呈周期性關係,這就導致了各種與材料態密度相關的物理量出現周期性的振盪現象—量子振盪，諸如電導或電阻隨磁場的變化產生的振盪，磁化率隨磁場的變化產生的振盪等等。根據波爾—索末菲條件,我們可以得 ( 其中 AF為費米面截面的極值) ，所以不同的量子振盪頻率反映著不同的費米面截面的極值。從而通過磁場方向的改變得到不同角度下量子振盪的頻率，就能得到該單晶材料的費米面的形狀 。如果該材料具有多個頻率，則我們應採用快速傅立葉變化( FFT) 來對所得到的量子振盪數據進行分析，如圖一( a) 、( b) 所示。