![重心[物理學術語]](/img/d/8c5/nBnauM3XzcTO2EDN2EDM3IDN0UTMyITNykTO0EDMwAjMwUzLxAzLxczLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg "重心[物理學術語]")
定義
物體各部分所受重力之合力的作用點。物體的每一微小部分都受地心引力作用（見萬有引力），這些引力可近似地看成為相交於地心的匯交力系。由於物體的尺寸遠小於地球半徑，所以可近似地把作用在一般物體上的引力視為平行力系，物體的總重量就是這些引力的合力。
如果物體的體積和形狀都不變，則無論物體對地面處於什麼方向，其所受重力總是通過固定在物體上的坐標系的一個確定點，即重心。重心不一定在物體上，例如圓環的重心就不在圓環上，而在它的對稱中心上。
重心位置在工程上有重要意義。例如，起重機要正常工作，其重心位置應滿足一定條件，艦船的浮升穩定性也與重心的位置有關；高速旋轉機械，若其重心不在軸線上，就會引起劇烈的振動等。
位置確定
物體的重心位置，質量均勻分布的物體（均勻物體），重心的位置只跟物體的形狀有關。有規則形狀的物體，它的重心就在幾何中心上，例如，均勻細直棒的中心在棒的中點，均勻球體的重心在球心，均勻圓柱的重心在軸線的中點。不規則物體的重心，可以用懸掛法來確定.物體的重心,不一定在物體上。
質量分布不均勻的物體，重心的位置除跟物體的形狀有關外，還跟物體內質量的分布有關。載重汽車的重心隨著裝貨多少和裝載位置而變化，起重機的重心隨著提升物體的重量和高度而變化。
過重心的一條直線或切面把物體或圖形分成兩份，則兩份的體積或面積不一定相等。（不是所有過重心的直線或切面都平分物體或圖形的面積或體積，例如過正三角形重心且平行一邊的一條直線把三角形分成面積比為4：5的兩部分。關於這一點，可以用物理學的槓桿原理解釋：分成的兩塊圖形的重心分別到三角形重心的距離相當於槓桿的兩個力臂，而兩圖形的面積相當於槓桿的兩個力。因為重心相當於兩個圖形的面積“集中”成的一點（參考重心定義）。如以上的例子，分割成的兩個圖形重心分別到三角形重心的距離正好等於5：4。如有興趣，可用尺規作圖證明。）
物體重心位置的數學確定方法：
在某物體（總質量為M）所在空間任取一確定的空間直角坐標系O-xyz，則該物體可微元出i個質點，每個質點對應各自坐標(xi,yi,zi)及質量mi，
已知M=m1+m2+‥+mi，設該物體重心為G（X，Y，Z）
則X=(x1m1+x2m2+‥+ximi)/M
Y=(y1m1+y2m2+‥+yimi)/M
自製桿秤找重心Z=(z1m1+z2m2+‥+zimi)/M
檢測方法
三角形重心
重心是三角形三邊中線的交點，三線交一點可用燕尾定理證明。
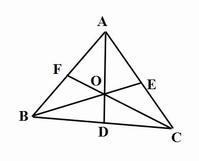三角形重心已知：△ABC中，D為BC中點，E為AC中點，AD與BE交於O，CO延長線交AB於F。求證：F為AB中點。
證明：根據燕尾定理，S(△AOB)=S(△AOC)，又S(△AOB)=S(△BOC)，∴S(△AOC)=S(△BOC)，再套用燕尾定理即得AF=BF，命題得證。
重心的幾條性質：
1.重心到頂點的距離與重心到對邊中點的距離之比為2：1。
2.重心和三角形3個頂點組成的3個三角形面積相等。
3.重心到三角形3個頂點距離的平方和最小。
4.在平面直角坐標系中，重心的坐標是頂點坐標的算術平均，即其坐標為((X1+X2+X3)/3,(Y1+Y2+Y3)/3)；空間直角坐標系——橫坐標：(X1+X2+X3)/3縱坐標：(Y1+Y2+Y3)/3 豎坐標：（Z1+Z2+Z3）/3
5.重心是三角形內到三邊距離之積最大的點。
6.(萊布尼茲公式)三角形ABC的重心為G，點P為其內部任意一點，則
3PG^2=(AP^2+BP^2+CP^2)-1/3(AB^2+BC^2+CA^2)
7.在三角形ABC中，過重心G的直線交AB、AC所在直線分別於P、Q，則 AB/AP+AC/AQ=3
8.從三角形ABC的三個頂點分別向以他們的對邊為直徑的圓作切線，所得的6個切點為Pi，則Pi均在以重心G為圓心，r=1/18(AB^2+BC^2+CA^2)為半徑的圓周上
![重心[物理學術語]](/img/d/153/wZwpmL1MTM5gjMzQDM1ATN0UTMyITNykTO0EDMwAjMwUzL0AzLzUzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg)
重心[物理學術語]如果用塞瓦定理證，則極易證三條中線交於一點。
如圖，在△ABC中，AD、BE、CF是中線
則AF=FB，BD=DC，CE=EA
∵(AF/FB)*(BD/DC)*(CE/EA)=1
∴AD、BE、CF交於一點
即三角形的三條中線交於一點
其它圖形重心
註：下面的幾何體都是均勻的，線段指細棒，平面圖形指薄板。
三角形的重心就是三邊中線的交點。線段的重心就是線段的中點。
平行四邊形的重心就是其兩條對角線的交點，也是兩對對邊中點連線的交點。
平行六面體的重心就是其四條對角線的交點，也是六對對棱中點連線的交點，也是四對對面重心連線的交點。
圓的重心就是圓心，球的重心就是球心。
錐體的重心是頂點與底面重心連線的四等分點上最接近底面的一個。
四面體的重心同時也是每個定點與對面重心連線的交點，也是每條棱與對棱中點確定平面的交點。
尋找重心方法
![重心[物理學術語]](/img/c/1af/wZwpmL1cjNzQDNxAzM1ATN0UTMyITNykTO0EDMwAjMwUzLwMzL4UzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg)
重心[物理學術語]下面是一些尋找形狀不規則或質量不均勻物體重心的方法。
a.懸掛法
只適用於薄板（不一定均勻）。首先找一根細繩，在物體上找一點，用繩懸掛，劃出物體靜止後的重力線，同理再找一點懸掛，兩條重力線的交點就是物體重心。
b.支撐法
只適用於細棒（不一定均勻）。用一個支點支撐物體，不斷變化位置，越穩定的位置，越接近重心。
一種可能的變通方式是用兩個支點支撐，然後施加較小的力使兩個支點靠近，因為離重心近的支點摩擦力會大，所以物體會隨之移動，使另一個支點更接近重心，如此可以找到重心的近似位置。
c.針頂法 同樣只適用於薄板。用一根細針頂住板子的下面，當板子能夠保持平衡，那么針頂的位置接近重心。
與支撐法同理，可用3根細針互相接近的方法，找到重心位置的範圍，不過這就沒有支撐法的變通方式那樣方便了。
d.用鉛垂線找重心（任意一圖形，質地均勻）
用繩子找其一端點懸掛，後用鉛垂線掛在此端點上（描下來）。而後用同樣的方法作另一條線。兩線交點即其重心。
重心計算
詳見參考資料
重心公式
詳見參考資料
