重心[幾何術語]

數學上的重心是指三角形的三條中線的交點，其證明定理有燕尾定理或塞瓦定理，套用定理有梅涅勞斯定理、塞瓦定理。

證明

已知：△ABC中，D為BC中點，E為AC中點，AD與BE交於O，CO延長線交AB於F。求證：F為AB中點。

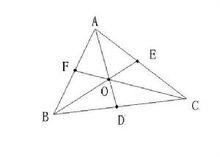圖1

證明1：燕尾定理：S(△AOB)=S(△AOC)，又S(△AOB)=S(△BOC)，∴S(△AOC)=S(△BOC)，

再套用燕尾定理即得AF=BF，命題得證。

證明2：塞瓦定理：如圖1，在△ABC中，AD、BE、CF是中線，則AF=FB，BD=DC，CE=EA。

∵(AF/FB)*(BD/DC)*(CE/EA)=1 ∴AD、BE、CF交於一點

即三角形的三條中線交於一點 。

性質

重心的幾條性質 ：

1.重心到頂點的距離與重心到對邊中點的距離之比為2：1。

2.重心和三角形3個頂點組成的3個三角形面積相等。

3.重心到三角形3個頂點距離的平方和最小。

4.在平面直角坐標系中，重心的坐標是頂點坐標的算術平均。

5.重心是三角形內到三邊距離之積最大的點。

6.三角形ABC的重心為G，點P為其內部任意一點，則3PG²=(AP²+BP²+CP²)-1/3(AB²+BC²+CA²)。

7.在三角形ABC中，過重心G的直線交AB、AC所在直線分別於P、Q，則 AB/AP+AC/AQ=3

8.從三角形ABC的三個頂點分別向以他們的對邊為直徑的圓作切線，所得的6個切點為Pi，則Pi均在以重心G為圓心，r=1/18(AB²+BC²+CA²)為半徑的圓周上。

9、G為三角形ABC的重心,P為三角形ABC所在平面上任意一點，則PA²+PB²+PC²=GA²+GB²+GC²+3PG²。

重心確定方法

對於均質物體，如在幾何形體上具有對稱面、對稱軸或對稱中心，則該物體的重心或形心必在此對稱面、對稱軸或對稱中心上。下面介紹幾種常用的確定重心位置的方法。
1.組合法
工程中有些形體雖然比較複雜，但往往是由一些簡單形體的組合，這些形體的重心通常是已知的或易求的。
2.負面積法
如果在規則形體上切去一部分，例如鑽一個孔等，則在求這類形體的重心時，可以認為原形體是完整的，只是把切去的部分視為負值（負體積或負面積）。

3.實驗法（平衡法）
如物體的形狀不是由基本形體組成，過於複雜或質量分布不均勻，其重心常用實驗方法來確定。主要包括懸掛法和稱重法。

重心的套用

數學套用

⑴求線段長

例 1　如圖2所示，在Rt△ABC中，∠A=30°，點D是斜邊AB的中點，當G是Rt△ABC的重心，GE⊥AC於點E，若BC=6cm，則GE的長度 。

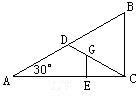圖2

解：Rt△ABC中，∠A=30°，BC=6 ∴AB=BC=12，

D是斜邊AB的中點，∴CD=1/2AB=6，

G是Rt△ABC的重心，∴CG=2/3CD=4，

由CD=AD，∠A=30°，∠GCE=30°。

Rt△GCE中，∠GCE=30°，CG=4，∴GE=1/2CG=2（cm）

⑵求面積

例 2 　在△ABC中，中線AD、BE相交於點O，如圖3，若△BOD的面積等於5，求△ABC的面積 。

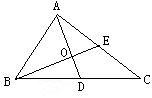圖3

解：∵O是△ABC的重心，∴AO∶OD=2∶1，

∴S∶S=2∶1， 即S=2 S=10，

∴S= S+ S=10+5=15，

又∵AD是△ABC的中線， S=2 S=30。

工程套用

重心在工程中具有重要的意義。例如，水壩的重心位置關係到壩體在水壓力作用下能否維持平衡；飛機的重心位置設計不當就不能安全穩定地飛行；構件截面的重心（形心）位置將影響構件在載荷作用下的內力分布規律，與構件受力後能否安全工作有著緊密的聯繫。總之，重心與物體的平衡、物體的運動以及構件的內力分布是密切相關的。