簡介
在航天動力學和宇宙空間動力學中,所謂的重力助推(也被稱為重力彈弓效應或繞行星變軌)是利用行星或其他天體的相對運動和引力改變飛行器的軌道和速度,以此來節省燃料、時間和計畫成本。重力助推既可用於加速飛行器,也能用於降低飛行器速度。原理解釋
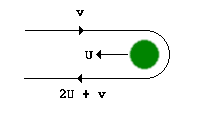
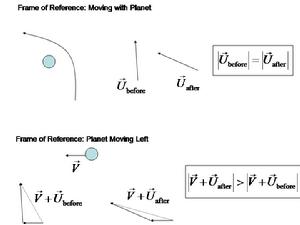
行星的重力助推作用能夠改變飛行器相對於太陽的速度,但由於必須遵守,所以它和行星間的相對速度並沒有改變。在飛行器第一次從遠距離接近行星時,產生的運動效果就像該飛行器被行星反彈開了。科學家們稱這種情況為彈性碰撞,不過兩者之間並沒有發生實體接觸。假設你是一個靜止的觀測者,那么你就會看到:行星以速度U向左運動,飛行器以速度v向右運動。由於兩者的運動方向相反,所以當飛行器運行至行星右側時,其軌道就會發生彎曲,進而以U+v的相對速度(相對於行星表面)運行。當飛行器脫離環行星軌道時,其相對於行星表面的速度仍然為U+v,但是此時的運動方向與原來相反——即向左運動。而由於行星本身正以速度U向左運動,所以在觀測者看來,飛行器正以2U+v的速度向左運行——其速度提升幅度為2U,即行星運行速度的兩倍。
由於未考慮軌道的各種細節,所以這是一個過於簡單化的模型。但是事實證明如果飛行器沿雙曲線軌道運行,則其無需啟動引擎既可從相反方向離開行星,同時只要其脫離了該行星引力的控制,那么它就可以獲得2U的加速度。
該理論看似違背了能量守恆和動量守恆定律,但這是由於我們忽略了飛行器對行星的影響。飛行器獲得的線性動量在數值上等同於行星失去的線性動量,不過由於行星的巨大質量,使得這種損失對其速度的影響可以忽略不計。
同時,重力助推也能被用於降低飛行器的速度。1974年的水手10號以及後來的信使號即通過重力助推實現了減速,兩者都是飛往水星的探測器。
如果飛行器需要獲得更多的加速度,最經濟的做法是當其位於行星近拱點時點燃火箭。火箭助推為飛行器提供的加速度總是相同的,但是它引起的動能變化則與飛行器的實時速度成正比。所以為了從火箭助推中獲得最大動能,火箭必須在飛行器速度最大時——即處於近拱點時點火。在奧伯特效應中該技術得到了詳細闡釋。
重力助推法的歷史淵源
最初提出重力助推法的科學家是蘇聯的尤里·康德拉圖克(Кондратюк, Юрий Васильевич)。他在所署時間為‘1918-1919’ 的論文‘Тем кто будет читать, чтобы строить’(《致有志於建造星際火箭而閱讀此文者》) 中提出在兩顆行星間飛行的飛船可以使用兩行星衛星的重力實現軌道初段的加速和軌道末段的減速。弗里德里希·詹德(Friedrich Zander)在其1925年的論文‘Проблема полета при помощи реактивных аппаратов: межпланетные полеты’(《星際飛行中噴氣推進的問題》) 中也提出了類似的構想。
但是兩者都未能意識到行星沿飛行器軌道施加的重力助推能夠推進飛行器從而減少飛行器星際間飛行的燃料消耗。 這一構想由麥可·米諾維奇(Michael Minovitch)於1961年提出。
1959年,重力推進法得到了首次套用,當時蘇聯的偵測器月球3號使用該法運行至月球背面並拍攝了該區域的照片。當時這一操作流程由克爾德什套用數學研究所所設計。
重力助推法的局限
兩個局限
在實際操作中,使用重力助推法的主要局限是行星和其他大質量天體並不總是在助推的理想的位置上。例如70年代末旅行者號得以成行的重要原因是當時木星、土星、天王星和海王星都將運行至助推的理想地點,形成了一個佇列。類似的佇列將要到22世紀中期才會再次出現。這是一個極端的例子,但是即使是某些目標較小的計畫,為了等待行星到達理想的位置,也必須空耗去數年時間。該方法的另一局限是提供重力助推的行星的大氣。由於重力與距離的平方成反比,所以當飛行器越接近行星時,其所獲得的重力助推效果就越顯著。但是如果飛行器太過於接近行星,從而過於深入行星大氣,那么其損耗的能量將會大於其從行星重力助推中獲得的能量。
相關探討
當然,從另一方面說,該效應也能夠用來實現大氣制動。也有人提出(至今還只是停留於理論階段)當飛行器穿越大氣層時可以利用大氣層的氣動升力為飛行器提供大氣推進力。該方法能夠將飛行器的軌道撓曲為一個較之重力助推更大的角度,因此也能夠獲取更多的動能。使用太陽作為行星間重力助推的天體是不可能的,因為太陽相對於太陽系整體來說是相對靜止的。但是,接近太陽時所獲得的強大推進也和重力推進由相似的效果。該方法能夠極大增加飛行器的動能,但是存在著飛行器是否能夠抵禦太陽高溫的問題。
而對於星際間的旅行,使用太陽作為重力助推的星體是可行的,如原本屬太陽系內的天體就可在飛掠太陽時獲得推進從而開始它的銀河系之旅,其能量和角動量來自於太陽環繞銀河運轉的軌道。但是這種星際間旅行所需的時間是超出人類可接受範圍的。
該方法的另一個理論上的限制是廣義相對論。如果飛行器接近黑洞的史瓦西半徑,它就需要更多的能量才能從這個極度扭曲的空間中逃逸出來,所耗的能量將會多於從黑洞的重力助推中獲得的能量。
不過,如果一個轉動的黑洞的自轉軸指向理想的方向,它就有可能提供額外的重力助推效果。廣義相對論預言一個較大的轉動天體的附近會出現參考系拖拽現象,即附近的空間被拖拽往天體自轉的方向。理論上一顆普通的恆星也會出現這種現象,但是對太陽附近空間所作的觀測至今未能得出確定的結果。廣義相對論預言在轉動的黑洞附近圍繞著一層被稱為能層的空間。在這個空間中物體的正常狀態仍然無法存在,因為該空間正沿著黑洞自轉方向以光速被拖拽著運動。但是潘洛斯機制或許可以為飛行器從能層中獲取能量,雖然這個過程要求飛行器必須將一些‘壓倉物’拋入黑洞,這樣飛行器也必須損失一部分由‘壓倉物’所攜帶的能量,這部分能量則被黑洞吸收。
