定義
都卜勒效應指出,波在波源移向觀察者時接收頻率變高,而在波源遠離觀察者時接收頻率變低。這種位移現象稱為都卜勒位移。
在日常生活中,我們都會有這種經驗:當一列鳴著汽笛的火車經過某觀察者時,他會發現火車汽笛的聲調由高變低. 為什麼會發生這種現象呢?這是因為聲調的高低是由聲波振動頻率的不同決定的,如果頻率高,聲調聽起來就高;反之聲調聽起來就低.這種現象稱為都卜勒效應,它是用發現者克里斯蒂安·都卜勒的名字命名的,都卜勒是奧地利物理學家和數學家.他於1842年首先發現了這種效應。為了理解這一現象,就需要考察火車以恆定速度駛近時,汽笛發出的聲波在傳播時的規律.其結果是聲波的波長縮短,好像波被壓縮了.因此,在一定時間間隔內傳播的波數就增加了,這就是觀察者為什麼會感受到聲調變高的原因;相反,當火車駛向遠方時,聲波的波長變大,好像波被拉伸了。因此,聲音聽起來就顯得低沉。
測量原理
散射面強度
雷射都卜勒信號的散射面是正弦信號。因為調製散射面的異常形狀,振幅正弦信號隨機變化,如圖所示。通過截取一個間隔來研究信號。在實驗中,對範圍間隔中的信號進行採樣並輸入電腦。 通過採樣,信號被轉換成n維點空間。 如果採樣後的雷射都卜勒信號可以表示為
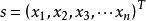 都卜勒位移
都卜勒位移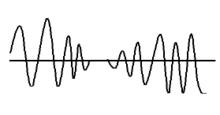 信號丟失
信號丟失在n維陣列空間中可以定義雷射都卜勒信號的強度:
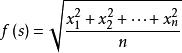 都卜勒位移
都卜勒位移由於f(n)是n維數組空間的一個常數,所以表達式可以被規範的定義驗證。
關係
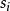 都卜勒位移
都卜勒位移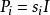 都卜勒位移
都卜勒位移 都卜勒位移
都卜勒位移 都卜勒位移
都卜勒位移簡化散射光接收部分差分都卜勒光學系統如圖所示。根據斑點原理如果透鏡的面積表示為S;這個區域的斑點粒子數是N;觀察表面的光的平均強度是I;第i個斑點顆粒的面積是 ,粒子光的平均功率是 ,散射光的相位是 ,透鏡的直徑是 ,然後聚焦在光電檢測器的感光表面上的總光功率可以表示為(w是都卜勒角速度):
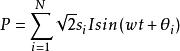 都卜勒位移
都卜勒位移通常,光電探測器的輸出V(t)與輸入功率成正比:
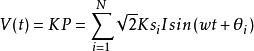 都卜勒位移
都卜勒位移這裡V(t)是隨機變數,K是比例常數(它與頻譜和設備的靈敏度等有關)。
如果散射面光斑的形狀為圓形,直徑為D,則可以從斑點原理得知:
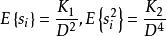 都卜勒位移
都卜勒位移其中E是平均值符號。 K和K是與表面粗糙度有關係的常數。 光電檢測器的輸出均方值為:
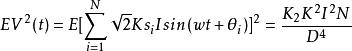 都卜勒位移
都卜勒位移因此,光電接收機的輸出均方根值為:
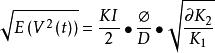 都卜勒位移
都卜勒位移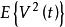 都卜勒位移
都卜勒位移因為隨機過程V(t)是遍歷的,並且如果V(t)在被採樣之後變換成離散值,並且如果n是非常大的數,則 表示為:
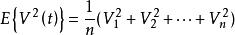 都卜勒位移
都卜勒位移均方根值為:
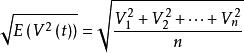 都卜勒位移
都卜勒位移這是由n維陣列空間中定義的飛彈表示的都卜勒信號的強度。
因此,差分都卜勒系統信號的強度f(s)表達為:
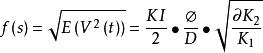 都卜勒位移
都卜勒位移我們可以看到收斂斑點的直徑較小,接收散射的透鏡直徑光線越大,光電接收機越敏感,都卜勒信號的強度越明顯。
差分系統
差分都卜勒光學系統套用於遠程面內位移測量如圖所示設計採用。
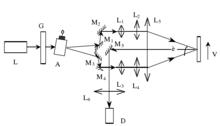 都卜勒位移
都卜勒位移該系統利用高斯波束的圖像理論,使L,L,L,L和L的圖像在L,L的焦平面上進行準直和擴展,然後收斂於移動物體O。參數為:入口高斯光束的腰部半徑為ω10= 1mm,焦距為F1 = F3 = 5mm,F2 = F4 = 100mm,F5 = 100m,透鏡L1-L5是校正的球面像差和塗覆的多層膜(反射鏡M1-M5),並且波長為ë= 632.8nm。該圖像距離由成像公式計算。
當被測物移動時的速度ν,散射光的都卜勒頻率被描述為:
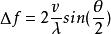 都卜勒位移
都卜勒位移通過對拍子信號的脈衝數N進行計數,物體O的位移x可以是:
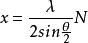 都卜勒位移
都卜勒位移很明顯,測量精度取決於會聚角度θ,θ越大,重疊區域的θ越小,位移測量精度越高。

