簡介
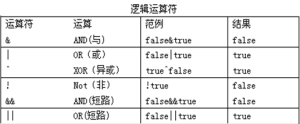
邏輯NOT邏輯AND
邏輯OR
優先權為:NOTANDOR
同級運算從左到右
| 例子 | 名稱 | 結果 |
|---|---|---|
| $a and $b | And(邏輯與) | TRUE,如果 $a 與 $b 都為 TRUE。 |
| $a or $b | Or(邏輯或) | TRUE,如果 $a 或 $b 任一為 TRUE。 |
| $a xor $b | Xor(邏輯異或) | TRUE,如果 $a 或 $b 同位相異。 |
| ! $a | Not(邏輯非) | TRUE,如果 $a 不為 TRUE。 |
| $a && $b | And(邏輯與) | TRUE,如果 $a 與 $b 都為 TRUE。 |
| $a || $b | Or(邏輯或) | TRUE,如果 $a 或 $b 任一為 TRUE。 |
基本運算符
 邏輯運算符
邏輯運算符注意,符號“與”(∧)和交集(∩),“或”(∨)和並集(∪)的相似性。這不是巧合:交集的定義使用“與”,並集的定義是用“或”。
這些連線符的真值表:
| P | Q | ¬ P | P∧與 Q | P∨或 Q | P→ Q | P↔ Q |
|---|---|---|---|---|---|---|
| T | T | F | T | T | T | T |
| T | F | F | F | T | F | F |
| F | T | T | F | T | T | F |
| F | F | T | F | F | T | T |
為了減少需要的括弧的數量,有以下的優先規則:¬高於∧,∧高於∨,∨高於→。例如,P∨Q∧¬R→S是(P∨(Q∧(¬R))→S的簡便寫法。

