基本介紹
還原問題是指已知一個數經過若干步運算後所得的結果,求原來這個數的套用題。解這類問題,可按題目所敘述的運算順序,利用加與減、乘與除的逆運算關係, 從已知的最後結果出發, 逐步逆推, 直至求得原數 。
這類問題的特點是:先提出某個未知量,經過一系列的已知的變化,最後給出另一已知數量,而求出原來的未知數量。解答這類問題的要點在於“還原”。從最後一個已知數出發,逐步逆推回去。原來加的,運算時用減;原來減的,運算時用加;原來乘的,運算時用除;原來除的,運算時用乘。列綜合算式計算時要注意運算順序,並且要正確使用括弧。這類問題叫還原問題 。
例題解析
【例1】某數加上6,減去5,乘以4,除以3,結果得248,求這個數。
解: 248×3÷4+5-6
=744÷4+5-6
=186+5-6=185
答:這個數是185。
【例2】一個小學生,計算一道算術題,應該用4.5去除,誤用4.5去乘了,結果得56.7。求正確的答案應該是多少 ?
解:由於誤用4.5去乘,結果得出56.7,那么未乘之前應該是什麼數?求出未乘之前的數之後,這個數按照題意用4.5去除,就是所求的答案。
56.7÷4.5=12.6(原數)
12.6÷4.5=2.8(正確答案)
答:正確的答案應該是2.8。
【例3】一位農民在集市上賣雞蛋,第一個顧客買去了全部雞蛋的一半零半個雞蛋;第二個顧客買去了剩下雞蛋中的一半零半個雞蛋;第三個顧客買去了最後剩下的15個雞蛋。這位農民去集市時一共帶了多少個雞蛋 ?
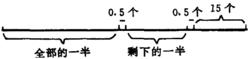 圖1
圖1解:半個雞蛋怎么能賣呢,使人覺得離奇。但是,這也並不奇怪。先通過幾個例子來說明。例如:3個雞蛋的一半是1.5個,再加上半個雞蛋,就是2個了;5個雞蛋的一半是2.5個;再加上半個雞蛋,就是3個了。凡是原有雞蛋的個數是奇數時,都可以這么說。
綜合算式:
[ (15+0.5)×2+0.5]×2=[31+0.5]×2=63 (個)
答:一共帶了63個雞蛋。
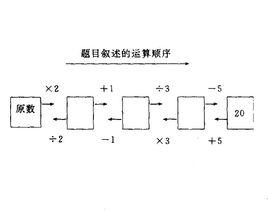
【例4】某數乘以2, 加1, 再除以3, 又減去5, 得20, 某數是多少 ?
此題的逆推過程如下圖所示:
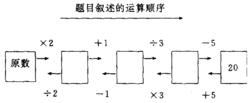 圖2
圖2解題的運算順序>列成算式是: [(20+5) ×3-1] ÷2=37。
還原問題, 也可能是已知幾個數經過若干組運算所得結果,求這幾個數。
【例5】有甲、乙、丙三個油桶,若盛油若干公斤,先將甲桶的油倒入乙、丙兩桶,使各增加原有油的一倍,再將乙桶的油倒入丙、甲兩桶,使它們現有的油各增加一倍, 最後同樣將丙桶的油倒入甲、乙兩桶,這樣各桶的油皆為16公斤,問各桶原來盛油多少公斤?
第三次倒油的結果是各桶都是16公斤, 那么當丙桶油未倒入甲、乙兩桶之前應該是甲桶16÷2=8 (公斤), 乙桶16÷2=8(公斤),丙桶16+8+8=32公斤。這就是第二次倒油的結果, 即乙桶油倒入甲、丙兩桶之後的結果,因此乙桶油未倒入甲、乙兩桶之前應該是:甲桶8÷2=4(公斤);丙桶32÷2=16 (公斤); 乙桶8+4+16=28 (公斤)。這就是第一次倒油的結果,即甲桶油倒入乙、丙兩桶之後的結果,因此各桶原來盛油應該是:乙桶28÷2=14 (公斤);丙桶16÷2=8 (公斤); 甲桶4+14+8=26 (公斤) 。