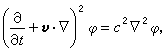運動媒質聲學
正文
研究運動媒質中的聲現象的學科。主要研究媒質運動對聲傳播的影響，和媒質運動時的發聲機制。運動媒質聲學的基本方程是
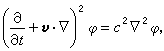(1)
exp(ik·r -iΩ t), (2)
其中r為隨著媒質一起運動的坐標；k為其中的波矢，其大小為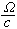
，而方向為波陣面法線方向 Ω呏ω/(1+Macosθ)＝ω-k·v (3)
為內稟頻率，即在隨著媒質一起運動的坐標系中所觀察到的(圓)頻率，這裡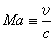
為媒質運動的馬赫數，θ為運動方向與波陣面法線之間的夾角，而 ω為靜止坐標系中所觀察到的頻率。式(3)描述了著名的都卜勒效應。從這裡也可看出，運動媒質中的波動現象（例如其中的聲速），依賴於傳播方向對運動方向的相對取向。也就是說，媒質的運動使它本身成為各向異性的，從而它的行為在許多方面類似於一單軸晶體,而運動速度v的方向相當於光軸方向。 在運動媒質聲學中，一些尋常的聲學關係得到相應的修正，例如在作平行運動的兩種媒質分界面上，尋常的折射定律被推廣為
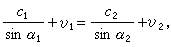
運動媒質的基本理論對於大氣聲學和水聲學，特別是前者中聲傳播的研究非常重要。但這時式（1）中的с和 v都不再是常數而是坐標(通常可認為只是鉛直坐標)的函式（稱為剖面）。在一定的剖面模型下，可用數值方法進行射線尋跡。
當媒質的運動不是理想的層流,而是隨機的湍流(例如實際大氣就經常處於這種狀態，見層流和湍流)時,聲波就不僅會有反射和折射，而且會有散射，同時其振幅、相位、頻率等都要產生起伏。
運動媒質聲學的另一主要內容是研究媒質運動時與其他物體相互作用以及其本身的發聲問題。
當流體衝擊到固體或邊界面上，在其附近產生一隨時間變化的壓力分布，結果就產生聲音。由此形成的聲源一般可用一個偶極子來近似。它所輻射的聲功率與流速的 6次方成正比。但對這種發聲機理的純理論分析相當困難，必須輔以關於相互作用力與描述流場各參量之間相互關係的實驗數據，在流體與固體相互作用而發聲的情形中，並不一定都必須是湍流。例如，物體在流體中作超聲速運動時以及系列物體（如螺旋槳）運動時都會輻射聲音。
即使不存在任何物體或邊界，隨時間變化的流場中也會產生壓力起伏，而這種壓力起伏引起小的密度起伏並象聲波那樣傳播開去。因此在任何情況下，流體中的不穩定區域都是一個聲源。這種聲源可以近似地用一個四極子（對偶極子）來描述，其所輻射的聲功率與流速的8次方成正比。
參考書目
P.M.摩爾斯、K.U.英格德著，楊訓仁等譯：《理論聲學》,下冊,第11章，科學出版社，北京，1986。(P. M.Morse and K. U. Ingard, Theoretical Acoustics, McGraw-Hill, New York,1968.)
