簡介
連通性分析是根據指定的起始和終止結點,分析兩點之間是否連通;或根據指定多個點,分析多個點之間是否互通。在計算機科學中,連通性分析主要是分析多個點之間連通性,在很多領域都有套用,例如圖論,電力網路設計,計算機網路之間連通性以及道路設計。通性分析方法主要有:鄰接矩陣法和樹搜尋法。
鄰接矩陣法
定義
鄰接矩陣(Adjacency Matrix):是表示頂點之間相鄰關係的矩陣。設G=(V,E)是一個圖,其中V={v1,v2,…,vn}。G的鄰接矩陣是一個具有下列性質的n階方陣:
①對無向圖而言,鄰接矩陣一定是對稱的,而且主對角線一定為零(在此僅討論無向簡單圖),副對角線不一定為0,有向圖則不一定如此。
②在有向圖中,任一頂點i的度為第i列(或第i行)所有非零元素的個數,在有向圖中頂點i的出度為第i行所有非零元素的個數,而入度為第i列所有非零元素的個數。
③用鄰接矩陣法表示圖共需要n^2個空間,由於無向圖的鄰接矩陣一定具有對稱關係,所以扣除對角線為零外,僅需要存儲上三角形或下三角形的數據即可,因此僅需要n(n-1)/2個空間。
分析
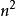 連通性分析
連通性分析鄰接矩陣法採用鄰接矩陣來描述拓撲圖中兩點之間的連通關係,直觀性比較好,但由於程式中的數據存儲空間開銷與節點數 n的平方成正比。在時間開銷上,它的運算次數是O( )級的。因此,當網路規模不大時,現有算法尚可承受;而當網路規模充分大時,用於連通性檢查的運算時間將隨節點數 n 的平方增長,因此這種算法將難以承受 。
樹搜尋法
樹搜尋法主要有廣度優先搜尋法和深度優先搜尋法。
廣度優先搜尋法
廣度優先搜尋算法(英語:Breadth-First-Search,縮寫為BFS),又譯作寬度優先搜尋,或橫向優先搜尋,是一種圖形搜尋算法。簡單的說,BFS是從根節點開始,沿著樹的寬度遍歷樹的節點。如果所有節點均被訪問,則算法中止。廣度優先搜尋的實現一般採用open-closed表。
BFS是一種盲目搜尋法,目的是系統地展開並檢查圖中的所有節點,以找尋結果。換句話說,它並不考慮結果的可能位址,徹底地搜尋整張圖,直到找到結果為止。BFS並不使用經驗法則算法。
從算法的觀點,所有因為展開節點而得到的子節點都會被加進一個先進先出的佇列中。一般的實現里,其鄰居節點尚未被檢驗過的節點會被放置在一個被稱為 open 的容器中(例如佇列或是鍊表),而被檢驗過的節點則被放置在被稱為 closed 的容器中。(open-closed表)。實現方法如下:
首先將根節點放入佇列中。
從佇列中取出第一個節點,並檢驗它是否為目標。
1.首先將根節點放入佇列中。
2.從佇列中取出第一個節點,並檢驗它是否為目標。
深度優先搜尋法
當搜尋總是沿著從父節點到子節點的方向不斷進行,直到無路可走時,才返回,這樣的搜尋方式叫做深度優先搜尋法。如果從節點P有可能到達節點C,則P叫做C的一個父節點,而C叫做P的一個子節點。如圖所示,深度優先搜尋,除搜尋失敗(即搜尋不到目標)而要求返回來搜尋原先被擱置的其他節點之外,在每一級只檢查一個節點。這種搜尋方法體現了優先向深度發展的趨勢,所以這種深度優先搜尋法又稱為縱向優先搜尋法。這裡需要提醒注意的是,深度優先搜尋是一個冒失而危險的方法。構想有更複雜的、樹形結構層次多得多的樹,在這樣的結構中進行深度優先搜尋過程,很容易出現滑過F節點的層次,而在窮盡下面的樹形結構中進行搜尋,這會浪費很多時間。對於這種樹結構此方法雖然容易實現,卻得到了最壞的可能路徑。當對複雜、多層次的樹形結構進行深度優先搜尋時,如果在離初始狀態相當遠的一段距離內搜尋不到目標,我們就希望沿原路返回,去試探其他一些路徑,而不繼續向前搜尋,以致離初始狀態太遠。在這種情況下,人們常常給搜尋樹規定一個深度界限,或稱最大深度。在考察一個節點時,如果其深度等於深度界限,就可不再向深度搜尋,而從原路返回,去探索其他路徑。這樣有時就可節約時間,儘快搜尋到目標。實現方法如下:
1. 首先將根節點放入佇列中。
2. 從佇列中取出第一個節點,並檢驗它是否為目標。
如果找到目標,則結束搜尋並回傳結果。
否則將它某一個尚未檢驗過的直接子節點加入佇列中。
3. 重複步驟2。
4. 如果不存在未檢測過的直接子節點。
將上一級節點加入佇列中。
重複步驟2。
5. 重複步驟4。
6. 若佇列為空,表示整張圖都檢查過了——亦即圖中沒有欲搜尋的目標。結束搜尋並回傳“找不到目標”。