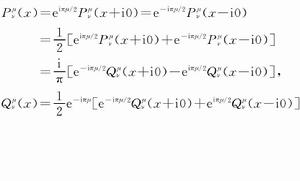定義
連帶勒讓德函式有兩類：第一類連帶勒讓德函式、第二類連帶勒讓德函式
連帶勒讓德函式是連帶勒讓德方程
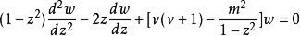連帶勒讓德函式
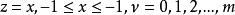連帶勒讓德函式
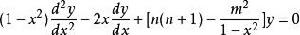連帶勒讓德函式的解，當 為任意整數的情形時，連帶勒讓德方程為 的一個解
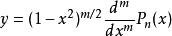連帶勒讓德函式
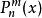連帶勒讓德函式
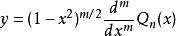連帶勒讓德函式記作 .另一個解為
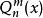連帶勒讓德函式記作 ，即
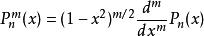連帶勒讓德函式
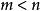連帶勒讓德函式.( )
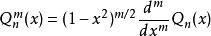連帶勒讓德函式 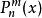連帶勒讓德函式 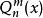連帶勒讓德函式， 分別稱為m階n次 第一類連帶勒讓德和 第二類連帶勒讓德函式。
第一類連帶勒讓德函式
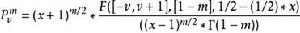連帶勒讓德函式
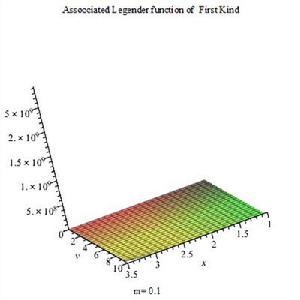第一類連帶勒讓德函式3D圖
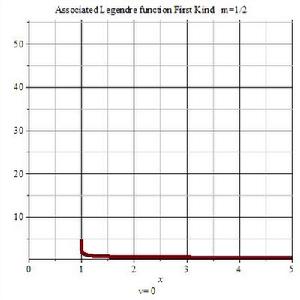第一類連帶勒讓德函式2D圖第二類連帶勒讓德函式
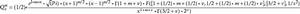連帶勒讓德函式
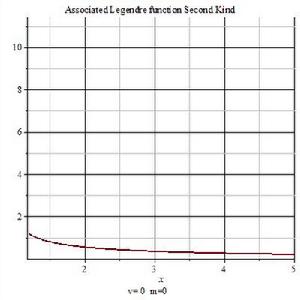第二類連帶勒讓德函式連帶勒讓德函式的母函式
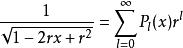連帶勒讓德函式由勒讓德多項式的母函式公式
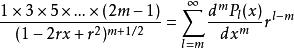連帶勒讓德函式兩次對x微分m次，得 .
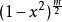連帶勒讓德函式
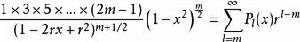連帶勒讓德函式兩端同乘以 ，得 .
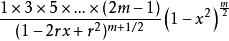連帶勒讓德函式
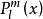連帶勒讓德函式因此， 即為連帶勒讓德函式 的母函式。
連帶勒讓德函式的遞推公式
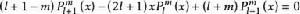連帶勒讓德函式(1) .
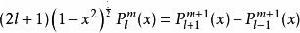連帶勒讓德函式(2) .
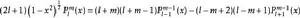連帶勒讓德函式(3) .
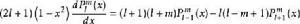連帶勒讓德函式(4) .
連帶勒讓德函式的正交歸一性
連帶勒讓德函式的正交歸一性是指
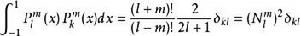連帶勒讓德函式
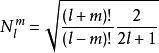連帶勒讓德函式 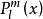連帶勒讓德函式其中， 稱為連帶勒讓德函式 的模。
連帶勒讓德函式的廣義傅立葉級數展開
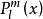連帶勒讓德函式 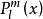連帶勒讓德函式連帶勒讓德函式 在區間[一1，1]上也構成一個正交完備系，可以看作廣義傅立葉級數展開的基函式。一個定義在區間[一1，1]上的連續函式，f(x)可展開成以連帶勒讓德函式 為基的廣義傅立葉級數
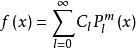連帶勒讓德函式
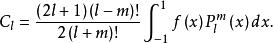連帶勒讓德函式其中廣義傅立葉係數為
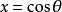連帶勒讓德函式若令 ,，則以上兩式可寫成
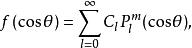連帶勒讓德函式
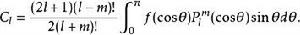連帶勒讓德函式